标签:两种 坐标 pre tin 规划 数组 例题 范围 不同
首先,我们先讲一下插头,总共6种双插头(一般用来解决回路问题和辅助单插头完成路径问题)和不知多少种单插头(用来解决路径问题)
别看插头多,其实大部分相同!
插头:

画得好丑
注:这只画了6种单插头,因为单插头在不同情况下可能会分(泌)出不同的情况,所以单插头难度比较大。
现在讲一下轮廓线:
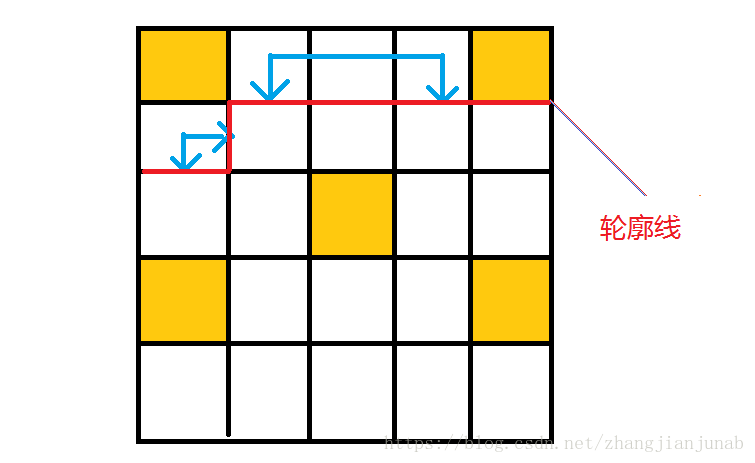
红不溜秋的东西十分重要!
如图,一条回路如同一大堆插头拼在一起!
括号表示法就是把轮廓线的状态用括号表示,从而压缩状态!
因为每一块(连在一起的插头)插头左右的要去扩张的插头会一直往下扩,所以不会出现左插头飞右插头右边
如:
所以,我们可以把左插头表示为左括号,右插头为右括号(一对),插头中的一部分或没插头为空。
但是,状态压缩呀,总不可能开个字符吧!那么,把左插头表示成1,右插头为2,空为0,每个数用两个二进制表示:01,10,00
然后,从左让右将二进制数合成一个大的数,用来表示当前状态!
如:
因为要包括没搞定的格子,所以轮廓线长度为m(矩阵宽度)+1
那么为什么要用二进制呢?位运算!
取出第轮廓线上的第q个位置的数:
int set(int s,int p)
{
return (s>>((p-1)*2))&3;
}改变第q位上的数为v:
void change(int &s/*引用,别打漏了*/,int p,int v)
{
s^=set(s,p)<<((p-1)*2);
s^=v<<((p-1)*2);
}不理解的同学搜一下C++的位运算理解一下!
其实,插头讲究的是分类讨论,对每种插头情况分类讨论!
先将Hash表,定一个inf和几个数组
定x,y,z,k分别%inf后得1 4 5 3
那么,得:
代码如下:
struct node
{
int hash[mod]/*压状态*/,key[mod]/*记录原本的数值*/,size/*记录存了多少数*/;ll num[mod]/*记录当前数值代表了多少状态*/;
void mem()
{
memset(hash,-1,sizeof(hash));size=0;//初始化函数
}
void add(int S,ll sum)
{
int s=S%mod;
while(hash[s]!=-1 && key[hash[s]]!=S)
{
s++;s%=mod;
}//判断重复,这样做是可以保证下次扔一个同样的数也可以到这个hash值
if(hash[s]==-1)
{
hash[s]=++size;key[size]=S;num[size]=sum;
}//新建一个hash格
else num[hash[s]]+=sum;//有的话直接加
}
}dp[2];//滚动数组有人会问:为什么同样的数值表示不用状态的方案数是可以加在一起的呢?
因为:
不管下面组成怎样,他们都可以接受,所以,他们的虽然样子不同,但状态相同,我们就可以把他们归为一类。
那么,接下来最难的其实是分类讨论,插头最难的就是因为它难调且容易漏了几种情况。
现在,我们设现在准备安上插头的格子从左面来的插头为q,上面来的为p。
如:
那么,我们就要利用q和p来分类讨论。。。就是代码。。。就不要在意了(一百多行)。
现在到转移状态了。
以这图为例:
因为这是一个障碍,所以只有当q=0并且p=0可以继承状态。
来个没障碍的:
那么,再讲两种比较难想的。
这种:
插头的概念就是可以延伸的插头一定会去延伸或和其他插头结合,但是什么时候结束呢?
就是当q=1并且p=2时且已经到最后一个非障碍格子时就可以将当前的状态记入状态。
但是!q=1并且p=2的情况不在最后一个非障碍格子时,就算一个废的情况(提前生成回路)。
为什么q=1并且p=2的情况一定生成回路呢?
如图:
那么最后一个格会不会不会出现一对的情况?(没有单插头)
只要有合法情况出现,因为插头的概念就是可以延伸的插头一定会去延伸或和其他插头结合,所以两个插头会一直延伸到最后一个格相遇!
就结束了。
上代码!
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;//不知道叫什么,感觉很大佬,就学了^_^
const int mod=200000;//hash表大小,因为hash表有压缩功能,所以一般100万就够了。
int map[50][50],n,m,ex=-1,ey=-1;//最后一个障碍格子的坐标
char ss[210];
ll ans=0;
struct node
{
int hash[mod],key[mod],size;ll num[mod];
void mem()
{
memset(hash,-1,sizeof(hash));size=0;
}//初始化
void add(int S,ll sum)
{
int s=S%mod;
while(hash[s]!=-1 && key[hash[s]]!=S)
{
s++;s%=mod;
}//找格子
if(hash[s]==-1)
{
hash[s]=++size;key[size]=S;num[size]=sum;
}
else num[hash[s]]+=sum;//将方案记录
}
}dp[2];
int now,php;
int set(int s,int p)
{
return (s>>((p-1)*2))&3;
}//取出第k个数
void change(int &s,int p,int v)
{
s^=set(s,p)<<((p-1)*2);
s^=(v&3)<<((p-1)*2);
}//改变
void work()
{
ll sum=0;
now=0;php=1;
dp[now].mem();
dp[now].add(0,1);//初始化滚动型DP数组
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
swap(now,php);
dp[now].mem();//滚动(dan)数组
for(int k=1;k<=dp[php].size;k++)
{
int s=dp[php].key[k];
sum=dp[php].num[k];
int q=set(s,j);
int p=set(s,j+1);
if(map[i][j]==0)
{
if(q==0 && p==0)dp[now].add(s,sum);
continue;
}//障碍格子
if(q==0 && p==0)
{
if(map[i+1][j]==1 && map[i][j+1]==1)//判断是否有障碍
{
change(s,j,1);change(s,j+1,2);//从这个格子建两个插头
dp[now].add(s,sum);
}
}//没人指我,只好自己建一个插头
else if(q>0 && p==0)
{
if(map[i+1][j]==1)dp[now].add(s,sum);//其实你拆开后简化就是这样子的
if(map[i][j+1]==1)//将插头引入右边,继承下去
{
change(s,j,0);change(s,j+1,q);
dp[now].add(s,sum);
}
}//继承
else if(q==0 && p>0)
{
if(map[i][j+1]==1)dp[now].add(s,sum);
if(map[i+1][j]==1)//将插头引入下边,继承下去
{
change(s,j,p);change(s,j+1,0);
dp[now].add(s,sum);
}
}//继承
else if(q==1 && p==1)
{
int find=1;//算上p为1!很重要。
for(int tt=j+2;tt<=m;tt++)//找到与p相对的右插头并修改为这一大块插头的左插头
{
int vs=set(s,tt);
if(vs==1)find++;
else if(vs==2)find--;//为什么可以?因为中间罩住的插头不会出去这个大插头的范围,所以只有碰到与p成对的插头才会清零
if(find==0)
{
change(s,j,0);change(s,j+1,0);change(s,tt,1);
dp[now].add(s,sum);
break;//你不加这个你试试
}
}
}
else if(q==2 && p==2)
{
int find=1;
for(int tt=j-1;tt>=1;tt--)//找到与q相对的左插头并修改为这一大块插头的右插头
{
int vs=set(s,tt);
if(vs==2)find++;
else if(vs==1)find--;//这样是不是太啰嗦了?
if(find==0)
{
change(s,j,0);change(s,j+1,0);change(s,tt,2);
dp[now].add(s,sum);
break;
}
}
}
else if(q==2 && p==1)//呵呵,这样的状态十分好想!因为对应的插头刚好也是我们想要的,只要把当前的q和p连接就好了!
{
change(s,j,0);change(s,j+1,0);
dp[now].add(s,sum);
}
else if(q==1 && p==2)
{
if(ex==i && ey==j)ans+=sum;//得到答案
}
}
}
for(int j=1;j<=dp[now].size;j++)dp[now].key[j]<<=2;//看下面解释
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",ss+1);
for(int j=1;j<=m;j++)
{
if(ss[j]==‘.‘){map[i][j]=1;ex=i;ey=j;}//这样做方便后面的判断
}
}
if(ex==-1){printf("0\n");return 0;}//特判
work();
printf("%lld\n",ans);//注意答案到了long long
return 0;
}在代码中只继承了合法方案,不合法方案已经被过滤了
估计许多人不理解这段
else if(q==2 && p==1)
{
change(s,j,0);change(s,j+1,0);
dp[now].add(s,sum);
}如图:
还有这段
for(int j=1;j<=dp[now].size;j++)dp[now].key[j]<<=2;因为每次完成一层,轮廓线都要下降一层,如:
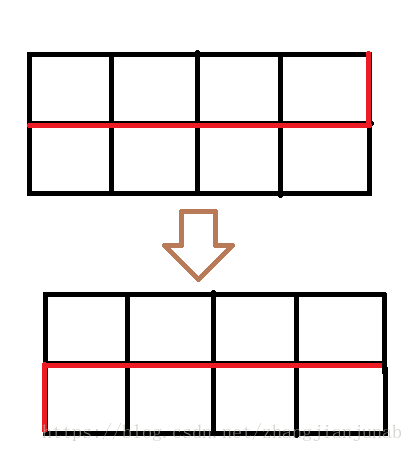
因为代码中判断矩阵外的格子为障碍,所以轮廓线最后那条竖线代表的是0,而且从下一行开始,一开始也没有插头指向开头那条竖线(总不可能在矩阵外开插头吧!),也为0,刚好每个状态(除了那条竖线外)也往后一位,所以,我们就把二进制往右移两位(因为每个括号要两个二进制数表示)来表示一层向下一层的转移!
那么,插头DP就解决啦!
猴子课堂:插头DP(基于连通性状态压缩的动态规划问题)(让你从入门到绝望)
标签:两种 坐标 pre tin 规划 数组 例题 范围 不同
原文地址:https://www.cnblogs.com/zhangjianjunab/p/9694676.html