标签：style blog http io os for sp 2014 on
按照顺时针或逆时针方向输入一个n边形的顶点坐标集，先判断这个n边形是否为凸包。
再给定一个圆形（圆心坐标和半径），判断这个圆是否完全在n变形内部。
1、判断凸包：
由于点集已经按某个时针方向有序，因此可以先定义一个方向系数direction=0
两两枚举n边形的边，用叉积判断这两条边的转向（右螺旋或左螺旋），由于存在散点共线的情况，因此当且仅当叉积的值temp第一次不为0时，direction=temp，direction的值此后不再改变。（direction>0 则为右螺旋逆时针，direction<0则为左螺旋顺时针）
此后继续枚举剩下的边，只要判断direction*temp>=0即可，当存在一个direction*temp<0的边，说明这是凹多边形，就不是凸包了。
2、判断圆心与多边形的关系：
用环顾法：
设圆心为P，逐条枚举n边形的边AB，利用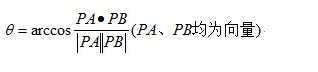
计算PA和PB的夹角，最后求和得到的就是环顾角。
（1） 圆心在多边形内部时，环顾角=±360
（2） 圆心在多边形外部时，环顾角=0
（3） 圆心在多边形边上时（不包括顶点），环顾角=±180
（4） 圆心在多边形顶点时，环顾角为(0,360)之间的任意角，其实就是圆心所在的顶点的两条邻接边的夹角。
3、当圆心在圆内时，判断圆与多边形的关系
设圆心为P，逐条枚举n边形的边AB，利用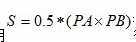
得到△PAB的面积，
再根据公式S=0.5*|AB|*h，可以得到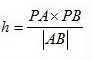
枚举所有h与圆的半径R比对，只要所有的边都有R-h>=0，则说明圆在多边形内
//Memory Time
//268K 0MS
#include<iostream>
#include<cmath>
using namespace std;
const double eps=1e-6;
const double pi=3.141592654;
typedef class NODE
{
public:
double x,y;
}pos;
int n;
double PegR; //钉子半径
pos Peg; //钉子坐标
int precision(double x); //精度讨论
double det(double x1,double y1,double x2,double y2); //叉积
double dotdet(double x1,double y1,double x2,double y2); //点积
double cross(pos A,pos B,pos C,pos D);
double distant(pos A,pos B); //计算距离
double angle(pos A,pos B,pos P); //计算向量PA与PB夹角
bool IsConvexBag(pos* Vectex); //判断输入的点集是否为凸包(本题保证了输入的点集为按某一时针方向有序)
bool IsIn(pos* Vectex); //判断圆心是否在多边形内部
bool IsFit(pos* Vectex); //判断圆的半径是否<=其圆心到多边形所有边的最小距离
int main(void)
{
while(cin>>n && n>=3)
{
cin>>PegR>>Peg.x>>Peg.y;
pos* Vectex=new pos[n+2]; //多边形顶点坐标
for(int i=1;i<=n;i++)
cin>>Vectex[i].x>>Vectex[i].y;
Vectex[0].x=Vectex[n].x; //封闭多边形，这样可以不用%运算
Vectex[0].y=Vectex[n].y;
Vectex[n+1].x=Vectex[1].x;
Vectex[n+1].y=Vectex[1].y;
if(!IsConvexBag(Vectex))
cout<<"HOLE IS ILL-FORMED"<<endl;
else
{
bool flag1=IsIn(Vectex);
bool flag2=IsFit(Vectex);
if(flag1 && flag2)
cout<<"PEG WILL FIT"<<endl;
else
cout<<"PEG WILL NOT FIT"<<endl;
}
delete Vectex;
}
return 0;
}
/*精度讨论*/
int precision(double x)
{
if(fabs(x)<=eps)
return 0;
return x>0?1:-1;
}
/*计算点积*/
double dotdet(double x1,double y1,double x2,double y2)
{
return x1*x2+y1*y2;
}
/*计算叉积*/
double det(double x1,double y1,double x2,double y2)
{
return x1*y2-x2*y1;
}
double cross(pos A,pos B,pos C,pos D)//cross(Vectex[i],Vectex[i+1],Vectex[i+1],Vectex[i+2])
{
return det(B.x-A.x , B.y-A.y , D.x-C.x , D.y-C.y);
}
/*计算距离*/
double distant(pos A,pos B)
{
return sqrt((B.x-A.x)*(B.x-A.x)+(B.y-A.y)*(B.y-A.y));
}
/*计算角度*/
double angle(pos A,pos B,pos P)
{
return acos(dotdet(A.x-P.x,A.y-P.y,B.x-P.x,B.y-P.y)/(distant(A,P)*distant(B,P)));
//点积，不是叉积
}
/*凸包判断*/
bool IsConvexBag(pos* Vectex)
{
int direction=0;
//保存点集Vectex的旋转方向direction 1:右手正螺旋，逆时针 -1:左手正螺旋，顺时针
for(int i=0;i<=n-1;i++)
{
int temp=precision(cross(Vectex[i],Vectex[i+1],Vectex[i+1],Vectex[i+2]));
if(!direction) //记录第一次偏转方向
direction=temp;
if(direction*temp<0) //只要Vectex是凸包，那么偏转方向始终一致，direction*temp都会>0，等于0表示直线情况4
return false;
}
return true;
}
/*判断点与多边形的关系*/
bool IsIn(pos* Vectex)
{
double CircleAngle=0.0; //环绕角
for(int i=1;i<=n;i++) //注意重复边不计算
if(precision(cross(Peg,Vectex[i],Peg,Vectex[i+1]))>=0)
CircleAngle+=angle(Vectex[i],Vectex[i+1],Peg);//不同方向偏的有正负区别
else
CircleAngle-=angle(Vectex[i],Vectex[i+1],Peg);
if(precision(CircleAngle)==0) //CircleAngle=0, Peg在多边形外部
return false;
else if(precision(CircleAngle-pi)==0 || precision(CircleAngle+pi)==0) //CircleAngle=正负180, Peg在多边形边上(不包括顶点)
{
if(precision(PegR)==0)//同时圆的半径是0
return true;
}
else if(precision(CircleAngle-2*pi)==0 || precision(CircleAngle+2*pi)==0) //CircleAngle=360, Peg在多边形边内部
return true;
else //CircleAngle=(0,360)之间的任意角， Peg在多边形顶点上
{
if(precision(PegR)==0)//同时圆的半径是0
return true;
}
return false;
}
/*判断圆与多边形的关系*/
bool IsFit(pos* Vectex)
{
for(int i=0;i<=n;i++)
{
int k=precision(fabs(cross(Peg,Vectex[i],Peg,Vectex[i+1])/distant(Vectex[i],Vectex[i+1]))-PegR);
if(k<0)//fabs(cross(Peg,Vectex[i],Peg,Vectex[i+1])即平行四边形面积
return false;
}
return true;
}
标签：style blog http io os for sp 2014 on
原文地址：http://www.cnblogs.com/notlate/p/4012961.html
