标签：img   关于   自由度   一个   才有   消失   取值   strong   17.   

1.点与坐标系

二维时：xy坐标和指向角度，例如扫地机器人，朝哪个方向运动 即 (x , y , θ )

向量的内积

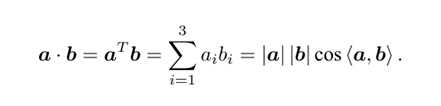
向量的外积

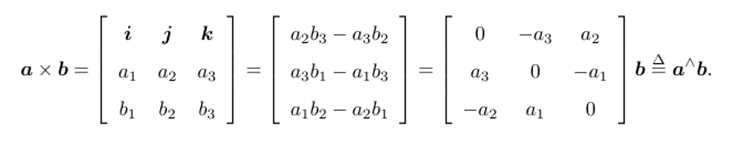
 a × b = a的反对称矩阵 点乘 b  =a ^ b   其中 a^ 为a的反对称矩阵

坐标系：世界坐标系，机器人坐标系，传感器坐标系

2.旋转矩阵

考虑旋转不考虑平移，一个固定点（坐标旋转否它就在那里），在两个坐标系的向量相等。

向量与坐标不能等同，当指定坐标系时，向量才有坐标，有实数对应。向量的坐标取值与向量和坐标系有关。

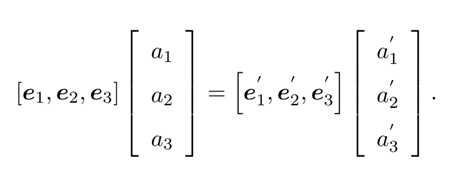
两边同时左乘一个向量，

使上式左边系数变成单位阵，即有

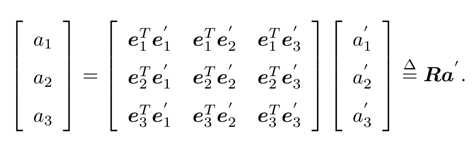
R为特殊正交群SO(3)。特殊正交群表示旋转，特殊欧式群SE(3) 表示变换即旋转+平移

性质：

有平移时

齐次形式

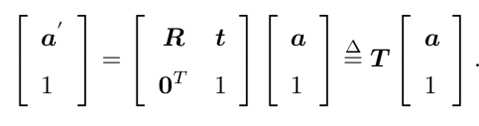
特殊欧式群

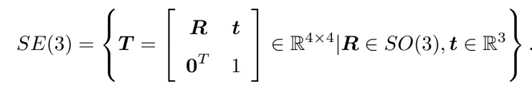
变换矩阵T的逆

3.旋转向量和欧拉角

旋转向量：

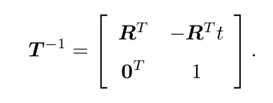
方向为旋转轴，长度为转过的角度

旋转向量到旋转矩阵的转换公式，罗德里格斯公式Rodrigues‘s Formula

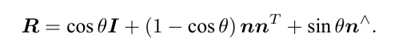
旋转矩阵到旋转向量

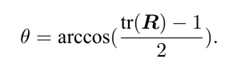
关于转轴n，旋转轴上的向量在旋转后不变，说明Rn=n。转轴n是矩阵R特征值1对应的特征向量。

欧拉角

将旋转分解为三个方向的转动

例如RPY roll pitch yall

想象飞机的飞行

1 绕Z轴旋转，得到偏航角yaw

2 绕旋转后的Y轴旋转，得到俯仰角 pitch

3 绕旋转后的X轴旋转，得到滚转角roll

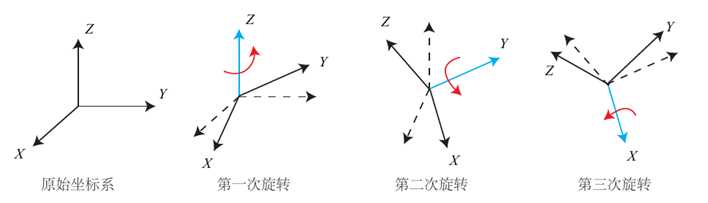
 欧拉角存在万向锁问题

存在奇异性，消失一个自由度

不适合插值和迭代，多用于人机交互，slam中少用

(1) 三维空间刚体运动

标签：img   关于   自由度   一个   才有   消失   取值   strong   17.   

原文地址：https://www.cnblogs.com/skyturtle/p/9696939.html