softmax 杂谈

标签：line   分类   def   pdb   dpi   ESS   python   inf   图片   

在多分类问题中，我们可以使用 softmax 函数，对输出的值归一化为概率值。下面举个例子：

import sys

sys.path.append("E:/zlab/")
from plotnet import plot_net, DynamicShow

num_node_list = [10, 7, 5]
figsize = (15, 6)
plot_net(num_node_list, figsize, ‘net‘)

Press `c` to save figure to "net.svg", `Ctrl+d` to break >>
> c:\programdata\anaconda3\lib\site-packages\viznet\context.py(45)__exit__()
-> plt.savefig(self.filename, dpi=300)
(Pdb) c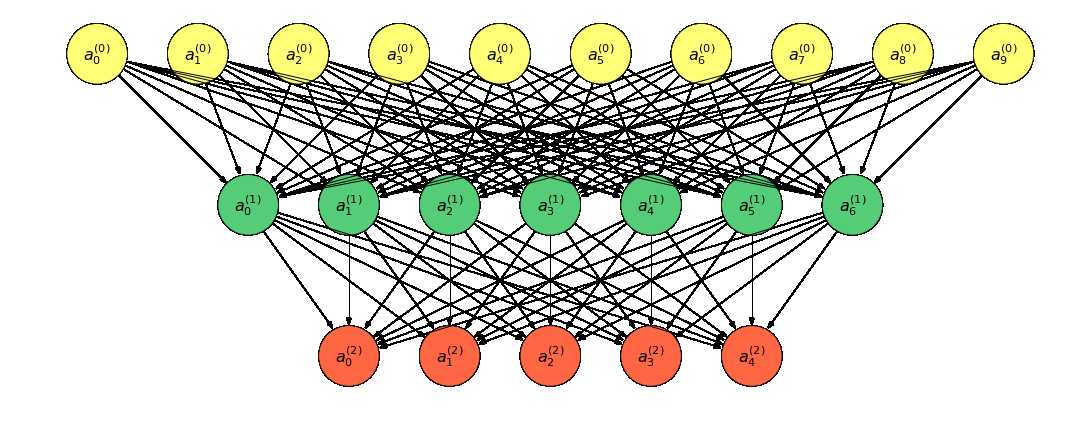

上图转换为表达式：

\[ \begin{aligned} &a^{(0)} = (a_0^{(0)}, a_1^{(0)}, \cdots, a_9^{(0)})^T\&a^{(1)} = (a_0^{(1)}, a_1^{(1)}, \cdots, a_6^{(1)})^T\&a^{(2)} = (a_0^{(2)}, a_1^{(2)}, \cdots, a_4^{(2)})^T\\end{aligned} \]

对于任意的 \(0 \leq i \leq 2\), 有前向传播的表达式：

\[ \begin{aligned} &z^{(i+1)} = W^{(i)}a^{(i)} + b^{(i)}\&a^{(i+1)} = f^{(i+1)}(z^{(i+1)}) \end{aligned} \]

其中，\(f^{(j)}\) 表示激活函数，除了输出层外，一般使用 ReLU 函数；\(W^{(i)}, b^{(i)}\) 为模型参数。

如若我们有 \(m\) 个样本 \(\{x^{(j)}\}_{j=1}^m\) 组成的数据集 \(D\), 称 \(X = (x^{(1)}, x^{(2)}, \cdots, x^{(m)})^T\) 为数据集 \(D\) 的设计矩阵。

这样，前向传播可以改写为：

\[ \begin{cases} Z^{(1+i)} = Z^{(i)}W^{(0)} + (b^{(i)})^T\A^{(1+i)} = f^{(1+i)}(Z^{(1+i)}) \end{cases} \]

• \(Z^{(i)} = (z_1^{(i)}, z_2^{(i)}, \cdots, z_m^{(i)})^T\), 这里对 \(z^{(i)}\) 添加下标以区别不同的样本;
• 这里对列向量 \(b^{(i)}\) 进行了 broadcast 操作;
• 且 \(Z^{(0)} = X\).

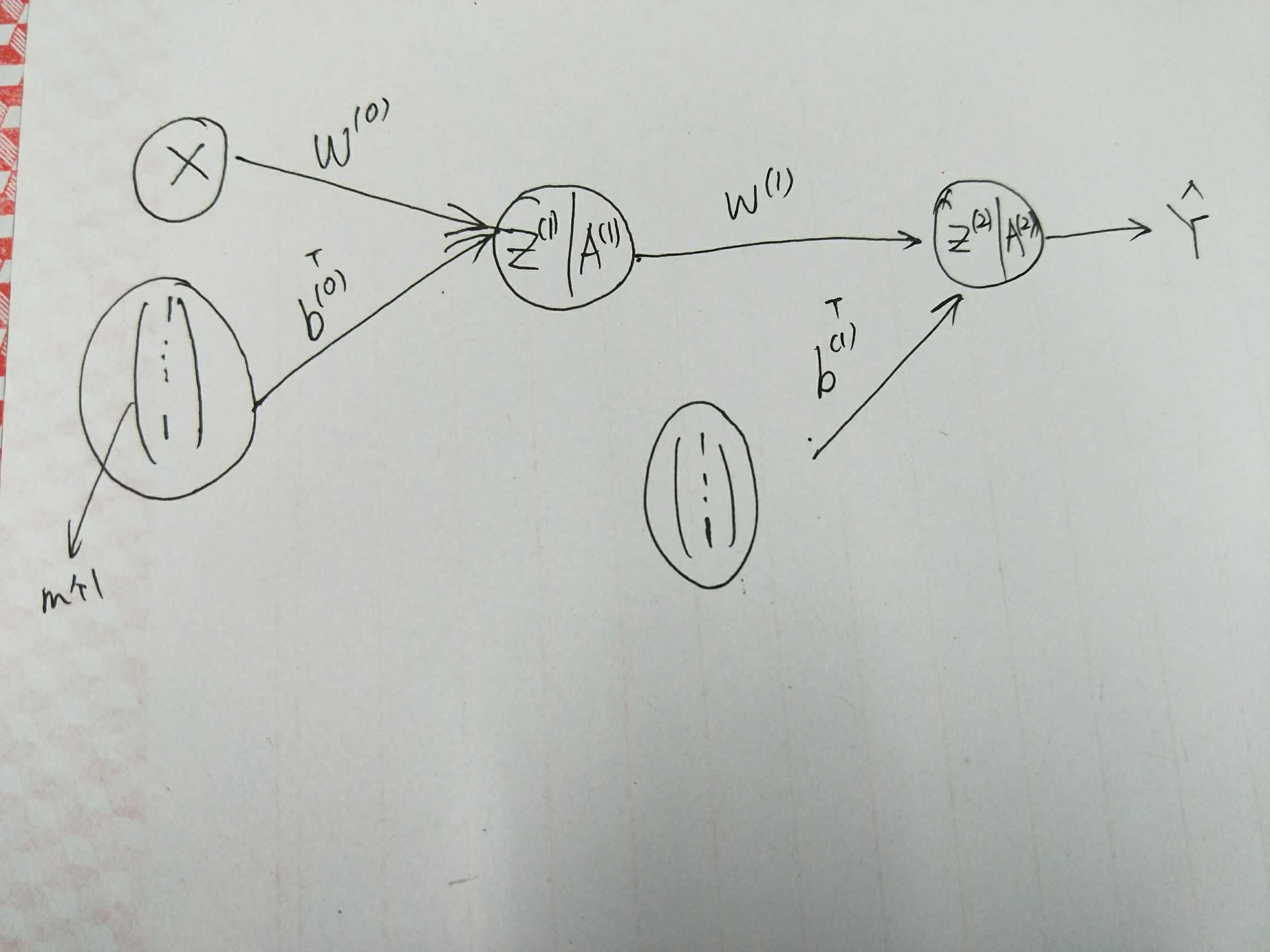
对于多分类问题，一般输出层对应的激活函数的 softmax 函数：

求解 \(A^{(2)}\):

1. 计算 \(exp = \exp(Z^{(1)})\);
2. 对 \(exp\) 按列做归一化, 便可得到 \(\text{softmax}(A^{(1)})\).

import numpy as np

def softmax(X):
    X_exp = np.exp(X)
    partition = X_exp.sum(axis=1, keepdims=True)
    return X_exp / partition  # 这里应用了广播机制。

softmax 杂谈

标签：line   分类   def   pdb   dpi   ESS   python   inf   图片   

原文地址：https://www.cnblogs.com/q735613050/p/9700656.html