标签:enter cal bubuko style script pre png close ||
Given a positive integers nn , Mobius function \mu(n)μ(n) is defined as follows:
\displaystyle \mu(n) = \begin{cases} 1 &n = 1 \\ (-1)^k & n = p_1p_2\cdots p_k \\ 0 &other \end{cases}μ(n)=??????1(−1)k0?n=1n=p1?p2??pk?other?
p_i (i = 1, 2, \cdots, k)pi?(i=1,2,?,k) are different prime numbers.
Given two integers mm, nn, please calculate \sum_{i = 1}^{m} \mu(in)∑i=1m?μ(in).
One line includes two integers m (1 \le m \le 2e9)m(1≤m≤2e9), n (1 \le n \le 1e12)n(1≤n≤1e12).
One line includes the answer .
2 2
-1
min_25筛的话,先得到下面这个公式
首先答案可以化简为这个
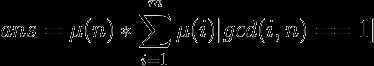
根据积性函数前缀和可以得到这个
(Sf(m,1)+1)*mu(n)
#include<bits/stdc++.h> using namespace std; #define ll long long const int N=1e6+5; ll p[N],w[N],pri[N],g[N],M,m,n; int block,id[N],sz,tot; bool is_p[N],v[N]; void init(int n) { sz=0; for(int i=2; i<=n; i++) { if(!is_p[i])p[++sz]=i; for(int j=1; j<=sz&&p[j]*i<n; j++) { is_p[i*p[j]]=1; if(i%p[j]==0) break; } } } void sieve_g(ll n) { M=0; for(ll i=1,lst; i<=n; i=lst+1) { ll len=n/i; lst=n/len; w[++M]=len; g[M]=1-w[M]; if(len<=block) id[len]=M; } for(int i=1; i<=sz; i++) for(int j=1; j<=M&&p[i]*p[i]<=w[j]; j++) { int op=w[j]/p[i]<=block?id[w[j]/p[i]]:n/(w[j]/p[i]); g[j]-=g[op]+i-1; } } ll S(ll x,ll y) { ll k,ans=0; if(x<=1||p[y]>x) return 0; if(x>block) k=m/x; else k=id[x]; ans=g[k]+y-1; for(int i=1; i<=tot&&pri[i]<=w[k]; i++) if(pri[i]>p[y-1]) ans++; for(int i=y; i<=sz&&p[i]*p[i]<=x; i++) if(v[i]==0) ans-=S(x/p[i],i+1); return ans; } int main() { tot=0; cin>>m>>n; block=sqrt(m+0.5); init(m<=1e6?1e4:1e6); sieve_g(m); for(int i=1; p[i]*p[i]<=n&&i<=sz;i++) { if(n%p[i])continue; pri[++tot]=p[i]; n/=p[i]; v[i]=1; if(n%p[i]==0) { puts("0"); return 0; } } if(n>1) { pri[++tot]=n; for(int i=sz; i>0; i--) if(p[i]==n) { v[i]=1; break; } } int t=tot&1?-1:1; cout<<(S(m,1)+1)*t; return 0; }
莫比乌斯+杜教筛
#include<bits/stdc++.h> using namespace std; #define ll long long const int N=1e6+5; int pri[N],num; int vst[N],mu[N],mu_n; inline void Pre() { mu[1]=1; for(int i=2; i<N; i++) { if(!vst[i]) pri[++num]=i,mu[i]=-1; for(int j=1; j<=num && i*1LL*pri[j]<N; j++) { vst[i*pri[j]]=1; if(i%pri[j]==0) { mu[i*pri[j]]=0; break; } mu[i*pri[j]]=mu[i]*mu[pri[j]]; } } for(int i=1; i<N; i++) mu[i]+=mu[i-1]; } unordered_map<ll,int> S; inline int Sum(ll n) { if(n<N) return mu[n]; if(S.count(n)) return S[n]; int tem=1; ll l,r; for(l=2; l*l<=n; l++) tem-=Sum(n/l); for(ll t=n/l; l<=n; l=r+1,t--) { r=n/t; tem-=(r-l+1)*Sum(t); } return S[n]=tem; } ll f(ll m,ll n) { if(m==0) return 0; if(n==1) return Sum(m); int flag=1; for(int i=1; pri[i]*1LL*pri[i]<=n; i++) { if(n%pri[i]==0) { flag=0; return -f(m,n/pri[i])+f(m/pri[i],n); } } if(flag)return -f(m,n/n)+f(m/n,n); } int judge(ll n) { for(int i=1; pri[i]*1LL*pri[i]<=n; i++) { if(n%pri[i]==0) { int cnt=0; while(n%pri[i]==0)n/=pri[i],cnt++; if(cnt>=2)return 0; } } return 1; } int main() { Pre(); ll m,n; cin>>m>>n; if(!judge(n)) { printf("0\n"); return 0; } cout<<f(m,n);; return 0; }
ACM-ICPC 2018 徐州赛区网络预赛 D. Easy Math
标签:enter cal bubuko style script pre png close ||
原文地址:https://www.cnblogs.com/BobHuang/p/9702972.html