As we all know, Matt is an outstanding contestant in ACM-ICPC. Graph problems are his favorite.
Once, he came up with a simple algorithm for finding the maximal independent set in trees by mistake.
A tree is a connected undirected graph without cycles, and an independent set is subset of the vertex set which contains no adjacent vertex pairs.
Suppose that the tree contains N vertices, conveniently numbered by 1,2, . . . , N. First, Matt picks a permutation p
1, p
2, . . . , p
N of {1, 2, 3, . . . , N } randomly and uniformly.
After picking the permutation, Matt does the following procedure.
1.Set S =
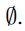
.
2.Consider the vertex p
1, p
2, . . . , p
N accordingly. For vertex p
i, if and only if there is no vertex in S which is adjacent to p
i, add vertex p
i into S.
3.Output the set S.
Clearly the above algorithm does not always output the maximal independent set. Matt would like to know the expected size of set S instead.
The first line contains only one integer T , which indicates the number of test cases.
For each test case, the first line contains an integer N (1 ≤ N ≤ 200), indicating the number of vertices in the graph.
Each of the following N - 1 lines contains two integers u, v (1 ≤ u, v ≤ N ) indicating an edge between u and v. You may assume that all the vertices are connected.
For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the answer. To avoid rounding error, the answer you should output is:
(the expected size of independent set) × N! mod (109 + 7)
2
4
1 2
1 3
1 4
3
1 2
2 3
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int a[maxn];
int main()
{
int t;
scanf("%d", &t);
for(int k = 1; k <= t; k++)
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
int min_a = a[n], ans = 0;
for(int i = n - 1; i > 0; i--)
{
if(a[i] > min_a) ans++;
else min_a = a[i];
}
printf("Case #%d: %d\n", k, ans);
}
return 0;
}
 .
.