标签:targe 获得 距离 个数 过程 size alt style dex
最小生成树的定义:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边,即n-1条边。
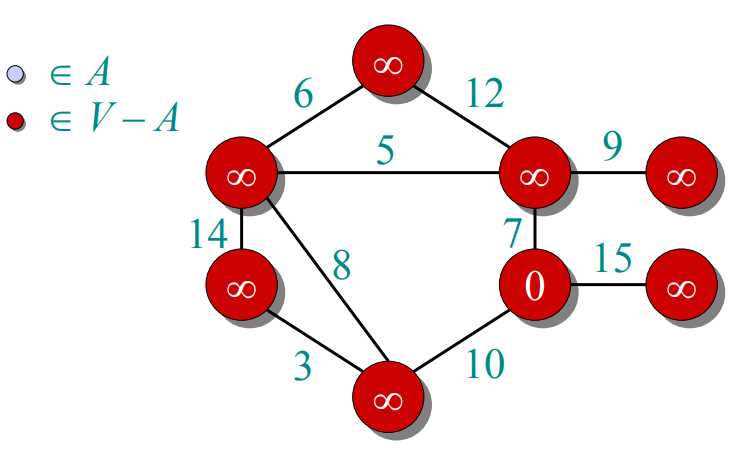
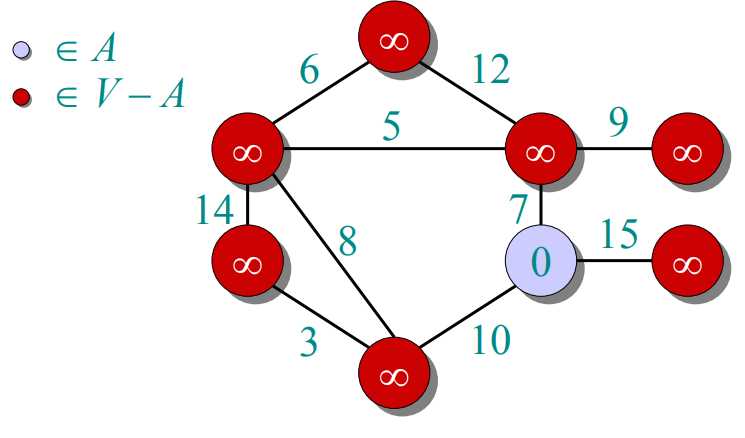
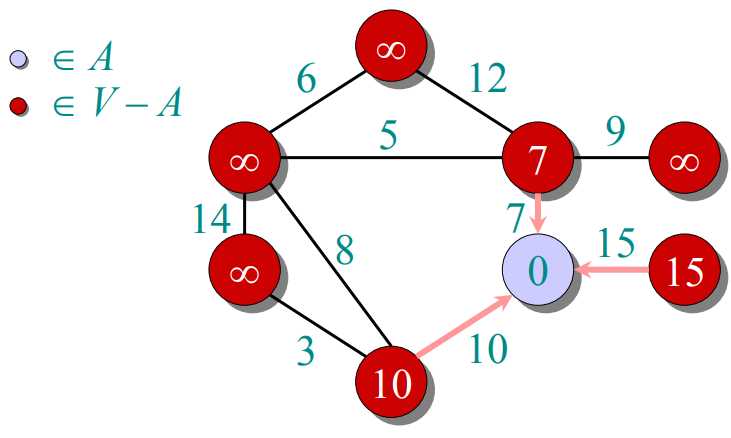
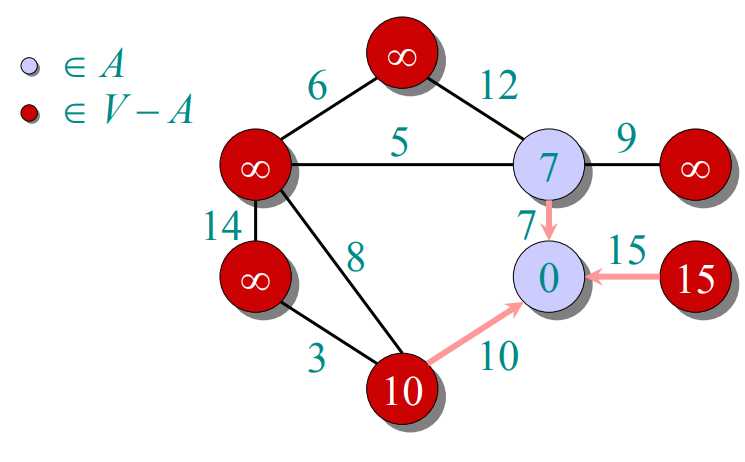
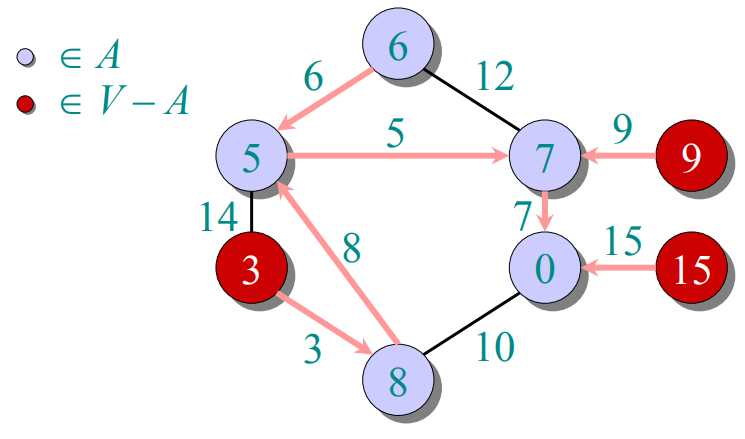
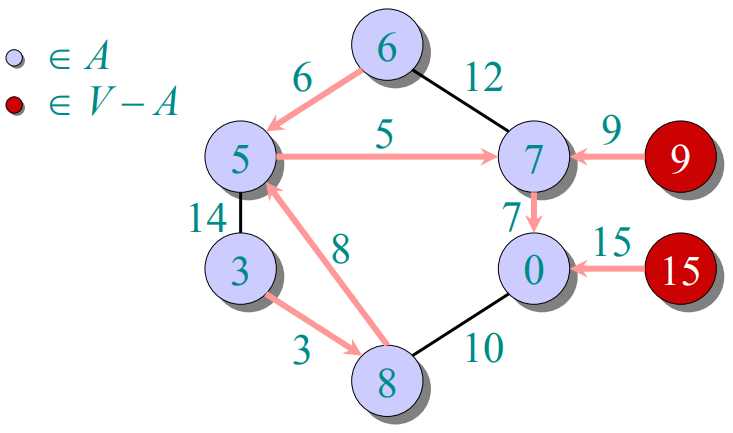
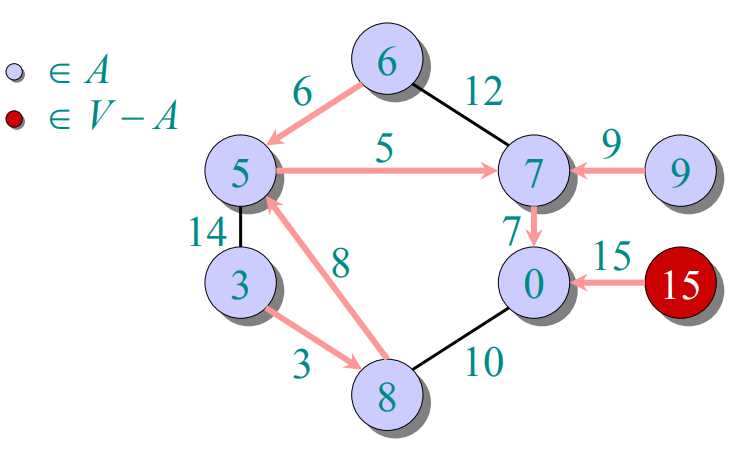
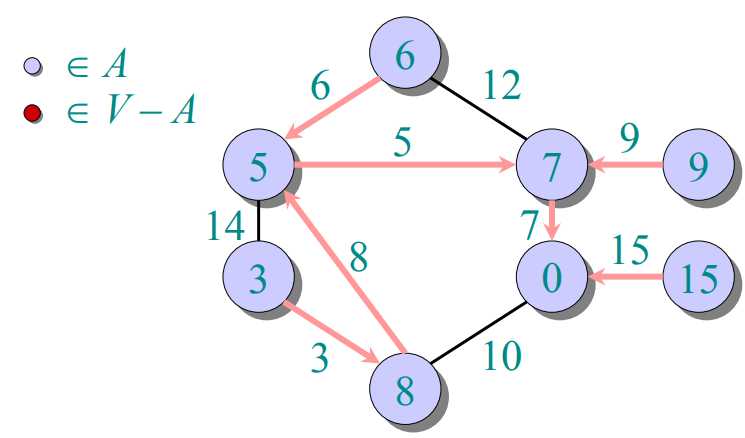
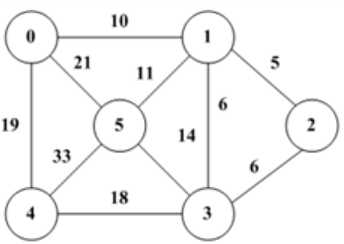
prim算法:把图中所有顶点放入集合V,每次往一个新的集合A中添加由A中顶点形成的图到V-A中顶点形成的图的最短距离对应的那个顶点(这个顶点在V-A中)。由于第一次添加时,A中是没有顶点的,也就是说随便添加哪个顶点都行。A中得到新的顶点后,更新V-A到A的距离。下一次添加最短距离对应的顶点(这个顶点在V-A中)。
过程如下图所示:
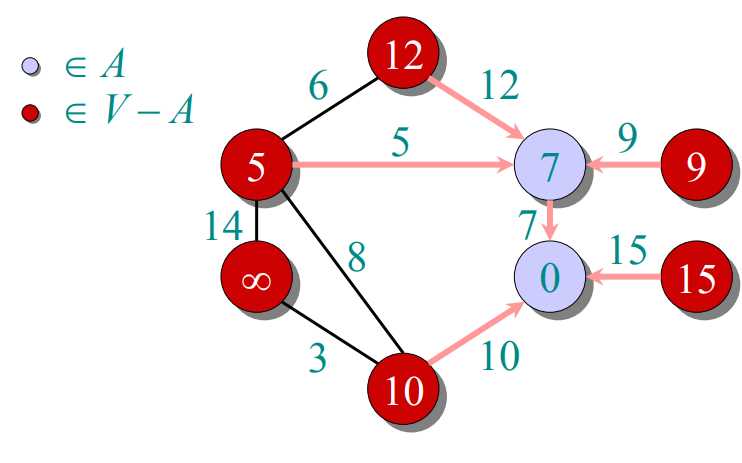
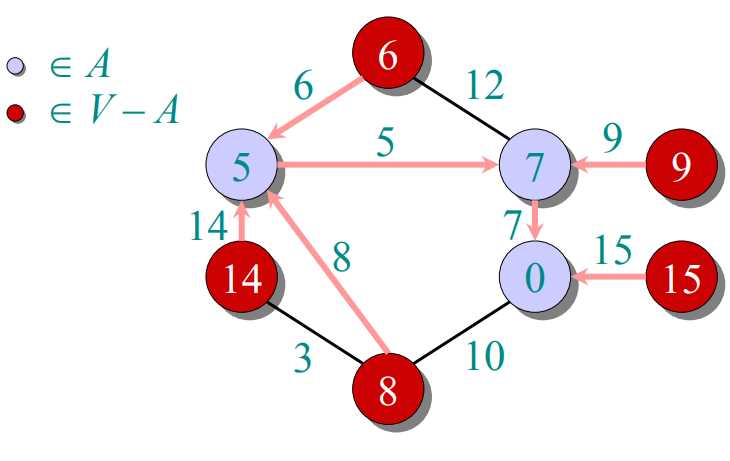
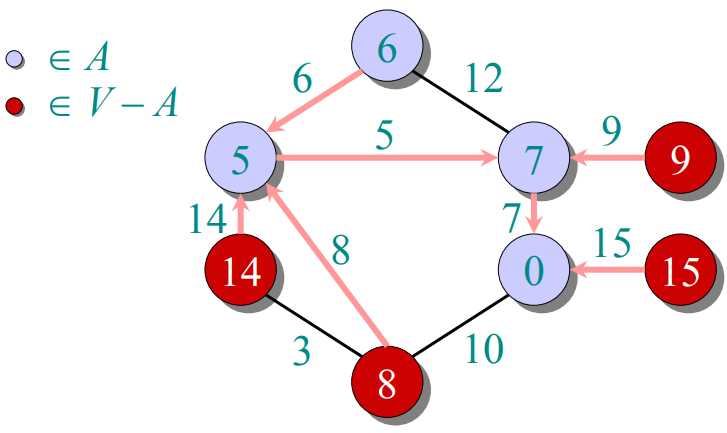
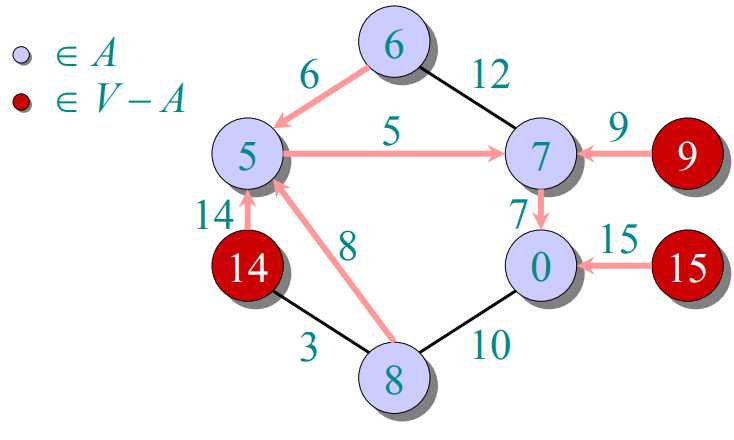
public class MST { //获得最小生成树,最小生成树顶点的信息封装在ArrayList中 public ArrayList<Node> getMST(int[][] graph,String[] arr) { Node min=null; //初始化集合V中的顶点 Node[] v=new Node[graph.length]; ArrayList<Node> a=new ArrayList<>(); for(int i=0;i<v.length;i++) { v[i]=new Node(); v[i].weight=999; v[i].value=arr[i]; v[i].key=i; } min=v[0]; //权值为-1表示该顶点已经加入到集合A中 min.weight=-1; a.add(min); //当集合A中的顶点个数与V中一样时,表示已经处理完所有的顶点 while(a.size()<graph.length) { for(int i=0;i<graph.length;i++) { //更新V-A中各顶点到A的距离 if(graph[min.key][i]<v[i].weight&&v[i].weight>0) { v[i].weight=graph[min.key][i]; v[i].pointTo=min; } } min=getMin(v); a.add(min); } return a; } //获取V-A中到A距离最小的顶点,并把他的权值置为-1表示该顶点加入到A中 public Node getMin(Node[] v) { int min=1000; int minIndex=-1; for(int i=0;i<v.length;i++) { if(v[i].weight<min&&v[i].weight>0) { min=v[i].weight; minIndex=i; } } v[minIndex].weight=-1; return v[minIndex]; } } //pointTo表示该顶点与哪个顶点相连,默认null. class Node{ String value; Node pointTo; int weight; int key; }
测试程序
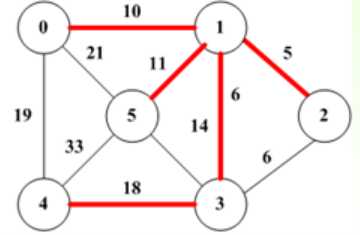
public class Test { public static void main(String[] args) throws Exception, SecurityException { String[] arr= {"0","1","2","3","4","5"}; int[][] graph= {{0,10,999,999,19,21}, {10,0,5,6,999,11}, {999,5,0,6,999,999}, {999,6,6,0,18,14}, {19,999,999,18,0,33}, {21,11,999,14,33,0}}; MST mst=new MST(); ArrayList<Node> node=mst.getMST(graph, arr); for(int i=1;i<node.size();i++) { System.out.println(node.get(i).value+"连接"+node.get(i).pointTo.value); } } }
结果:

标签:targe 获得 距离 个数 过程 size alt style dex
原文地址:https://www.cnblogs.com/javaStudy947/p/9715400.html