四则运算

时间：2018-09-28 11:00:10 阅读：200 评论：0 收藏：0 [点我收藏+]

github项目传送门：https://github.com/bpgg/FourArithmeticOperation

项目要求

　　- 功能列表

[完成] 使用 -n 参数控制生成题目的个数
[完成] 使用 -r 参数控制题目中数值的范围, 。该参数可以设置为1或其他自然数。
[完成] 生成的题目中计算过程不能产生负数
[完成] 生成的题目中如果存在形如e1 ÷ e2的子表达式，那么其结果应是真分数。
[完成] 程序一次运行生成的题目不能重复,生成的题目存入执行程序的当前目录下的Exercises.txt文件
[完成] 每道题目中出现的运算符个数不超过3个
[完成] 在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件
[完成] 程序应能支持一万道题目的生成。
[未完成] 程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计

PSP开发耗时

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30	60
· Estimate	· 估计这个任务需要多少时间	30	60
Development	开发	1000	2240
· Analysis	· 需求分析 (包括学习新技术)	100	180
· Design Spec	· 生成设计文档	60	100
· Design Review	· 设计复审 (和同事审核设计文档)	30	30
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	30
· Design	· 具体设计	120	150
· Coding	· 具体编码	600	1500
· Code Review	· 代码复审	50	60
· Test	· 测试（自我测试，修改代码，提交修改）	150	60
Reporting	报告	80	80
· Test Report	· 测试报告	30	60
· Size Measurement	· 计算工作量	20	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	20
合计		1110	2400

· 思路分析

- 生成表达式

　　使用对象存储子表达式，两个子表达式组成一个总表达式

　　表达式对象使用字符串类型存储操作数和操作符

　　控制表达式符号与数字之间保留一个空格，方便后续筛选

- 检查是否重复

　　每生成一个表达式都会添加到列表里面

　　通过遍历列表的表达式确定是否为相同的表达式子，如果是，重新生成表达。

- 存储表达式存储

　　将生成的中缀表达式转化为后缀表达式

　　根据运算优先级将操作数和符号存储在对应节点中

　　父节点存储运算符号，子节点存储操作数

　　例如： 3+2+1

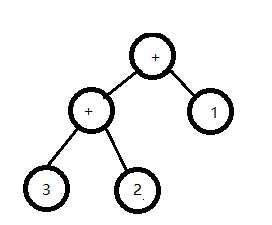
　　技术分享图片

- 计算表达式结果

　　根据表达式对应的二叉树进行计算，

　　将左右子节点进行操作之后把值赋给父节点

　　重复上述操作，直到根节点停止

　　根节点的值即为所求

　　并将所求值存储在答案列表里

- 写入文件

　　遍历表达式列表和答案列表

　　分别写入对应的文件

程序流程图

用户使用说明

举例：

-n [数值] 使用 -n 参数控制生成题目的个数。

-r [数值] 使用 -r 参数控制题目中数值（自然数、真分数和真分数分母）的范围。

代码

项目目录：

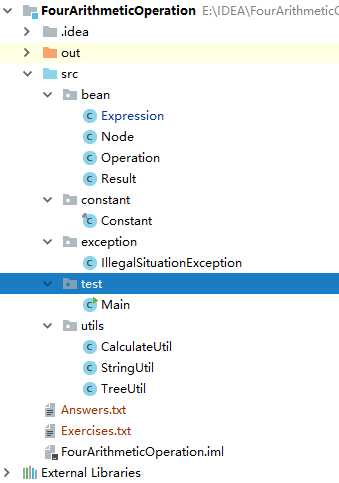
技术分享图片

生成表达式：

- 生成操作数

  public String generateOperand(int iRange)
    {
        String sOpreand="";


        switch(randomer.nextInt(3)) {
            case 0://生成带分数
                sOpreand = (randomer.nextInt(iRange)+1)+"’"+generatePrimes(iRange);
                break;
            case 1:
                sOpreand = generatePrimes(iRange);
                break;
            case 2:
                sOpreand =String.valueOf(randomer.nextInt(iRange)+1);
                break;
        }
        return sOpreand;
    }

- 生成分数（分子分母互质，无需约分）

b    private String generatePrimes(int iRange)
    {
        //分子最大为8
        int iNumerator=randomer.nextInt(iRange)+1;
        int iDenominator=iNumerator+randomer.nextInt(iRange)+1;

        //保证两个数互质
        if(iNumerator==0)
        {
            //分子为0，分母直接使用
            return iNumerator+"/"+iDenominator;
        }
        int comDivisor = getComDivisor(iNumerator, iDenominator);
        iNumerator/=comDivisor;
        iDenominator/=comDivisor;

        return iNumerator+"/"+iDenominator;
    }

- 数值互转及详细操作

  1 package utils;
  2 
  3 import exception.IllegalSituationException;
  4 
  5 public class CalculateUtil {
  6 
  7     //加法
  8 
  9     /**
 10      * 两个数的相加
 11      *
 12      * @param a 加数
 13      * @param b 加数
 14      * @return 结果
 15      */
 16     public static String add(String a, String b) {
 17         if (a.equals("0")||b.equals("0")){
 18             return a.equals("0")?b:a;
 19         }
 20         //两个都是自然数
 21         if (isNaturalNumber(a) && isNaturalNumber(b)) {
 22             return String.valueOf(Integer.valueOf(a) + Integer.valueOf(b));
 23         }
 24 
 25         //两个都是分数
 26         if (!isNaturalNumber(a) && !isNaturalNumber(b)) {
 27             String m = getRealFraction(a);
 28             String n = getRealFraction(b);
 29 
 30             return simplify(addFractionAndFraction(m, n));
 31 
 32         }
 33         //一个是自然数一个是分数
 34         if (isNaturalNumber(a) && !isNaturalNumber(b)) {
 35             String fraction = getRealFraction(b);
 36             return simplify(addFractionAndNatural(a, fraction));
 37         }
 38 
 39         //一个是分数一个是自然数
 40         if (!isNaturalNumber(a) && isNaturalNumber(b)) {
 41             String fraction = getRealFraction(a);
 42             return simplify(addFractionAndNatural(b, fraction));
 43         }
 44 
 45         return null;
 46 
 47     }
 48 
 49     /**
 50      * 分数加自然数 ，int[0] 为分子， int[1]  为分母
 51      *
 52      * @param natural  自然数
 53      * @param fraction 分数
 54      * @return 结果
 55      */
 56     private static String addFractionAndNatural(String natural, String fraction) {
 57         int nat = Integer.valueOf(natural);
 58         int[] numB = getDenominatorAndMolecule(fraction);
 59 
 60         int molecule = nat * numB[1] + numB[0];   //分子
 61         int denominator = numB[1];  // 分母
 62         return molecule + "/" + denominator;
 63     }
 64 
 65     /**
 66      * 两个分数相加 int[0] 为分子， int[1]  为分母
 67      *
 68      * @param a 加数
 69      * @param b 加数
 70      * @return 结果
 71      */
 72     private static String addFractionAndFraction(String a, String b) {
 73         int[] numA = getDenominatorAndMolecule(a);
 74         int[] numB = getDenominatorAndMolecule(b);
 75 
 76         int molecule = numA[0] * numB[1] + numB[0] * numA[1];
 77         int denominator = numA[1] * numB[1];
 78 
 79         return molecule + "/" + denominator;
 80 
 81     }
 82 
 83     //减法
 84 
 85     /**
 86      * 两个数的减法
 87      *
 88      * @param a 减数
 89      * @param b 被减数
 90      * @return 结果
 91      */
 92     public static String subtract(String a, String b) {
 93         if (a.equals("0")||b.equals("0")){
 94             return a.equals("0")? "-"+b:a;
 95         }
 96         //两个都是自然数
 97         if (isNaturalNumber(a) && isNaturalNumber(b)) {
 98             return String.valueOf(Integer.valueOf(a) - Integer.valueOf(b));
 99         }
100 
101         //两个都是分数
102         if (!isNaturalNumber(a) && !isNaturalNumber(b)) {
103             String m = getRealFraction(a);
104             String n = getRealFraction(b);
105 
106             return simplify(subtractFractionAndFraction(m, n));
107 
108         }
109         //一个是自然数一个是分数
110         if (isNaturalNumber(a) && !isNaturalNumber(b)) {
111             String fraction = getRealFraction(b);
112             return simplify(subtractFractionAndFraction(naturalToFraction(a, fraction), fraction));
113         }
114 
115         //一个是分数一个是自然数
116         if (!isNaturalNumber(a) && isNaturalNumber(b)) {
117             String fraction = getRealFraction(a);
118             return simplify(subtractFractionAndFraction(fraction, naturalToFraction(b, fraction)));
119         }
120 
121         return null;
122     }
123 
124     /**
125      * 自然数转分数 int[0] 为分子， int[1]  为分母
126      *
127      * @param natural  自然数
128      * @param fraction 分数
129      * @return 结果
130      */
131     private static String naturalToFraction(String natural, String fraction) {
132         int[] numFrac = getDenominatorAndMolecule(fraction);
133         int molecule = Integer.valueOf(natural) * numFrac[1]; //分子
134         int denominator = numFrac[1];  // 分母
135         return molecule + "/" + denominator;
136 
137     }
138 
139     /**
140      * 分数减分数 int[0] 为分子， int[1]  为分母
141      *
142      * @param a 分数
143      * @param b 分数
144      * @return 结果
145      */
146     private static String subtractFractionAndFraction(String a, String b) {
147         int[] numA = getDenominatorAndMolecule(a);
148         int[] numB = getDenominatorAndMolecule(b);
149 
150         int molecule = numA[0] * numB[1] - numB[0] * numA[1]; //分子
151         int denominator = numA[1] * numB[1];  //分母
152 
153         return molecule + "/" + denominator;
154     }
155 
156     //乘法
157 
158     /**
159      * 乘法
160      *
161      * @param a 乘数
162      * @param b 乘数
163      * @return 结果
164      */
165     public static String multiplies(String a, String b) {
166         if (a.equals("0")||b.equals("0")){
167             return String.valueOf(0);
168         }
169         //两个都是自然数
170         if (isNaturalNumber(a) && isNaturalNumber(b)) {
171             return String.valueOf(Integer.valueOf(a) * Integer.valueOf(b));
172         }
173 
174         //两个都是分数
175         if (!isNaturalNumber(a) && !isNaturalNumber(b)) {
176             String m = getRealFraction(a);
177             String n = getRealFraction(b);
178 
179             return simplify(multipliesFractionAndFraction(m, n));
180 
181         }
182         //一个是自然数一个是分数
183         if (isNaturalNumber(a) && !isNaturalNumber(b)) {
184             String fraction = getRealFraction(b);
185             return simplify(multipliesFractionAndFraction(naturalToFraction(a, fraction), fraction));
186         }
187 
188         //一个是分数一个是自然数
189         if (!isNaturalNumber(a) && isNaturalNumber(b)) {
190             String fraction = getRealFraction(a);
191             return simplify((multipliesFractionAndFraction(fraction, naturalToFraction(b, fraction))));
192         }
193         return null;
194     }
195 
196     /**
197      * 分数乘分数
198      *
199      * @param a 分数
200      * @param b 分数
201      * @return 结果
202      */
203     private static String multipliesFractionAndFraction(String a, String b) {
204         int[] numA = getDenominatorAndMolecule(a);
205         int[] numB = getDenominatorAndMolecule(b);
206 
207         int molecule = numA[0] * numB[0];  //分子
208         int denominator = numA[1] * numB[1];  // 分母
209 
210         return molecule + "/" + denominator;
211     }
212 
213     /**
214      *  除法
215      * @param a 除数
216      * @param b 被除数
217      * @return 结果
218      */
219     public static String divide(String a, String b) throws IllegalSituationException {
220         if (a.equals("0")){
221             return String.valueOf(0);
222         }
223         if (b.equals("0")){
224             throw new IllegalSituationException("Argument b can’t be zero");
225         }
226         //两个都是自然数
227         if (isNaturalNumber(a) && isNaturalNumber(b)) {
228             return simplify(a + "/" + b);
229         }
230 
231         //两个都是分数
232         if (!isNaturalNumber(a) && !isNaturalNumber(b)) {
233             String m = getRealFraction(a);
234             String n = getRealFraction(b);
235             return simplify(divideFractionAndFraction(m, n));
236 
237         }
238         //一个是自然数一个是分数
239         if (isNaturalNumber(a) && !isNaturalNumber(b)) {
240             String fraction = getRealFraction(b);
241             return simplify(divideFractionAndFraction(naturalToFraction(a, fraction), fraction));
242         }
243 
244         //一个是分数一个是自然数
245         if (!isNaturalNumber(a) && isNaturalNumber(b)) {
246             String fraction = getRealFraction(a);
247             return simplify(divideFractionAndFraction(fraction, naturalToFraction(b, fraction)));
248         }
249 
250         return null;
251     }
252 
253     /**
254      * 分数除分数
255      * @param a 除数
256      * @param b 被除数
257      * @return  结果
258      */
259     private static String divideFractionAndFraction(String a, String b) {
260         int[] numA = getDenominatorAndMolecule(a);
261         int[] numB = getDenominatorAndMolecule(b);
262 
263         int molecule = numA[0] * numB[1];
264         int denominator = numA[1] * numB[0];
265 
266         return molecule + "/" + denominator;
267     }
268 
269 
270     /**
271      * 获取分数的分子和分母
272      *
273      * @param a 分数
274      * @return 结果，int[0] 为分子， int[1]  为分母
275      */
276     private static int[] getDenominatorAndMolecule(String a) {
277         String numA[] = a.split("[/]");
278         int numInt[] = new int[numA.length];
279         for (int i = 0; i < numInt.length; i++) {
280             numInt[i] = Integer.valueOf(numA[i]);
281 
282         }
283         return numInt;
284     }
285 
286     /**
287      * 分数形式的转换
288      *
289      * @param s 分数
290      * @return 结果
291      */
292     private static String getRealFraction(String s) {
293         if (isFalseFraction(s)) { //1"1/2
294             String numStr[] = s.split("[’/]");
295             int numInt[] = new int[numStr.length];
296             for (int i = 0; i < numInt.length; i++) {
297                 numInt[i] = Integer.valueOf(numStr[i]);
298 
299             }
300             int denominator = numInt[0] * numInt[2] + numInt[1];
301             return denominator + "/" + numStr[2];
302         }
303 
304         return s;
305     }
306 
307     /**
308      * 判断是否为自然数
309      *
310      * @param s 数
311      * @return 结果
312      */
313     private static boolean isNaturalNumber(String s) {
314         return !s.contains("/");
315     }
316 
317     /**
318      * 判断是否为 假分数
319      *
320      * @param s 数
321      * @return 结果
322      */
323     private static boolean isFalseFraction(String s) {
324         return s.contains("’");
325     }
326 
327     private static String simplify(String fraction){
328         int[] num = getDenominatorAndMolecule(fraction);
329         int molecule = num[0] ;
330         int denominator = num[1] ;
331         if (molecule==0){
332             return String.valueOf(0);
333         }
334         if (molecule==denominator){
335             return "1";
336         }
337 
338         if (molecule<denominator){
339             int i ;
340             if ((i=gcd(molecule,denominator))==1){
341                 return molecule +"/" +denominator;
342             }
343             molecule = molecule/i;
344             denominator = denominator/i;
345             return molecule +"/" +denominator;
346         }
347 
348         if (molecule>denominator){
349            int i = gcd(molecule,denominator);
350            molecule = molecule/i;
351            denominator = denominator/i;
352 
353            if (denominator==1){
354                return molecule+"";
355 
356            }
357 
358            return getWithFraction(molecule,denominator);
359 
360         }
361 
362         return null;
363 
364     }
365 
366     /**
367      *  获取带分数 
368      * @param molecule 分子
369      * @param denominator 分母 
370      * @return 结果
371      */
372     private static String getWithFraction(int molecule,int denominator){
373         int withFraction = (molecule - (molecule%denominator)) / denominator;
374         molecule = molecule%denominator;
375         return withFraction+"’"+molecule+"/"+denominator;
376     }
377 
378     /**
379      *  求最大公约数，欧几里得方法
380      * @param m 数1
381      * @param n 数
382      * @return 结果
383      */
384     private static int gcd(int m, int n) {
385         return n == 0 ? m : gcd(n, m % n);
386     }
387 
388     public static boolean isNegative(String num){
389         return num.contains("-");
390     }
391 }

- 后缀表达式处理数据

public static String InfixToPostfix(String expression) {


        String str[] = expression.split("\\s+");

        for (String  s : str) {

            //四个操作符
            if (isOperator(s)) {
                handleOperator(s);
                continue;
            }
            //左括号，入栈
            if (s.equals("(")) {
                mStack.push(s);
                continue;
            }

            //右括号，弹出并输出，直到遇到左括号，左括号也弹出
            if (s.equals(")")) {

                while (!mStack.peek().equals("(")) {

                    mExp.append(mStack.pop());
                    mExp.append(" ");
                }
                mStack.pop();

                continue;
            }
            mExp.append(s);
            mExp.append(" ");


        }
        //栈中还有数据，直接出栈输出
        while (!mStack.empty()) {
            mExp.append(mStack.pop());
            mExp.append(" ");
        }

        return mExp.toString();


    }

- 输出表达式到Exercises.txt和输出答案到Answers.txt：

 private static void doWork(int iQuestions,int iRange){
        while (mList.size() != iQuestions) {

            String ex = Operation.generateQuestion();
            Node tree = TreeUtil.createTree(StringUtil.InfixToPostfix(ex));
            if (generate1(tree).isIllegal() && !isEquals(mResult)) {
                mResult.setExpression(ex);
                mList.add(mResult);
            }
        }

        //文件操作对象
        FileOutputStream outSTr1 ;
        FileOutputStream outSTr2 ;
        BufferedOutputStream Buff1;
        BufferedOutputStream Buff2;
        long begin0 = System.currentTimeMillis();
        try {
            outSTr1 = new FileOutputStream(new File(".\\Exercises.txt"));
            outSTr2 = new FileOutputStream(new File(".\\Answers.txt"));
            Buff1 = new BufferedOutputStream(outSTr1);
            Buff2 = new BufferedOutputStream(outSTr2);
            for(int i=0; i<mList.size();i++){
                Buff1.write(((i+1)+" 、"+mList.get(i).getExpression()+"\r\n").getBytes());
                Buff2.write(((i+1)+" 、"+mList.get(i).getResult()+"\r\n").getBytes());
            }
            Buff1.flush();
            Buff2.flush();
            Buff1.close();
            Buff2.close();
            long end0 = System.currentTimeMillis();
            System.out.println("BufferedOutputStream执行耗时:" + (end0 - begin0) + " 毫秒");
        } catch(Exception e){
            System.out.println("出现异常:" + e.getMessage());
        }

    }

测试运行

表达式的输出

-n 10 -e 10
9’9/10 + 6’6/11 × 9 - 6 = 62’89/110
5 × 3’1/7 = 15’5/7
3’1/9 - 1/2 = 2’11/18
9 + 10/17 + 2 × 9 = 27’10/17
9 + 2’3/13 ÷ 1/4 = 17’12/13
3’5/7 + 8 - 2 = 9’5/7
6’2/5 ÷ 9’3/4 ÷ 10’1/2 = 256/4095
4’1/5 + 6/11 ÷ 9 = 4’43/165
9’7/16 ÷ 3/7 - 5 = 17’1/48
2’6/13 × 2’5/14 = 5’73/91

- 随机输出10000条10范围以内的表达式和答案:

　　10000个答案

　　https://github.com/bpgg/FourArithmeticOperation/blob/master/src/Answers.txt

　　10000个表达式

　　https://github.com/bpgg/FourArithmeticOperation/blob/master/src/Exercises.txt

总结

在与马仪生的合作中，我体验到了直接调用别人写好的接口的快乐。在本次实验中，我主要负责生成表达式及总结，仪生主要负责处理表达式。在与仪生的合作中，我了解到更多编码规范，必须对象类的报名定义为bean，一些固定的常量也需要放在const包中，调用的工具类放在util包里，把各种功能实现分开实现，最后集中使用，便于维护的同时也是代码更加清晰。

四则运算

标签：随机学习 color lse 数加处理 mem ural order

原文地址：https://www.cnblogs.com/fyy30/p/9710972.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行