标签:递归 val end cto space sub bsp png ++
今天这题困扰了我好久,本来以为是自己dp写错了,结果wa了好多次以后发现原来是自己的处理输入这块出现了不知名的bug,所以干脆直接用结构体存了!!!
思路:动态规划的典型问题,将矩阵连乘积AiAi-1...Aj简记为A[i:j] ,i≤j 。
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,i≤k<j,则其相应完全加括号方式为:
(AiAi+1...Ak)(Ak+1Ak+2...Aj)
令m[i:j]为最优解,则m[i:k]和m[k+1:j]则为A[i:k]和A[k+1:j]的最优解,以此递归这得递归式:
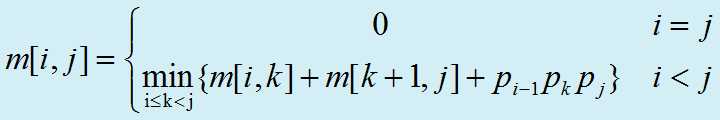
代码如下:
1 #include<iostream>
2 #include<cstring>
3 #include<algorithm>
4 #include<vector>
5 #define INF 999999999
6
7 using namespace std;
8
9 struct M
10 {
11 int x;
12 int y;
13 }m[1010];
14
15 int dp[1010][1010];
16 int solve(int n)
17 {
18 memset(dp,0,sizeof(dp));
19 for (int len = 2; len <= n; len++)
20 {
21 for(int i=1; i<=n-len+1; i++)
22 {
23 int j = i+len-1;
24 dp[i][j] = dp[i+1][j] + m[i-1].x*m[i-1].y*m[j-1].y;
25 for (int k = i+1; k < j; k++)
26 {
27 int count = dp[i][k] + dp[k+1][j] + m[i-1].x*m[k-1].y*m[j-1].y;
28 if (count < dp[i][j])
29 dp[i][j] = count;
30 }
31 }
32 }
33 return dp[1][n];
34 }
35 int main()
36 {
37 int n;
38 while(cin>>n)
39 {
40 bool falg=false;
41 for(int i=0; i<n; i++)
42 {
43 cin>>m[i].x>>m[i].y;
44 }
45 for(int i=0; i<n-1; i++)
46 {
47 if(m[i].y != m[i+1].x)
48 {
49 falg = true;
50 break;
51 }
52 }
53 if(!falg)
54 {
55 cout<<solve(n)<<endl;
56 }
57 else
58 cout<<"invalid argument"<<endl;
59
60 }
61 return 0;
62 }
标签:递归 val end cto space sub bsp png ++
原文地址:https://www.cnblogs.com/kerman/p/9726875.html