标签:ISE 广度优先 linked 一个 com 记录 lis span 图片
一、题目
1、审题
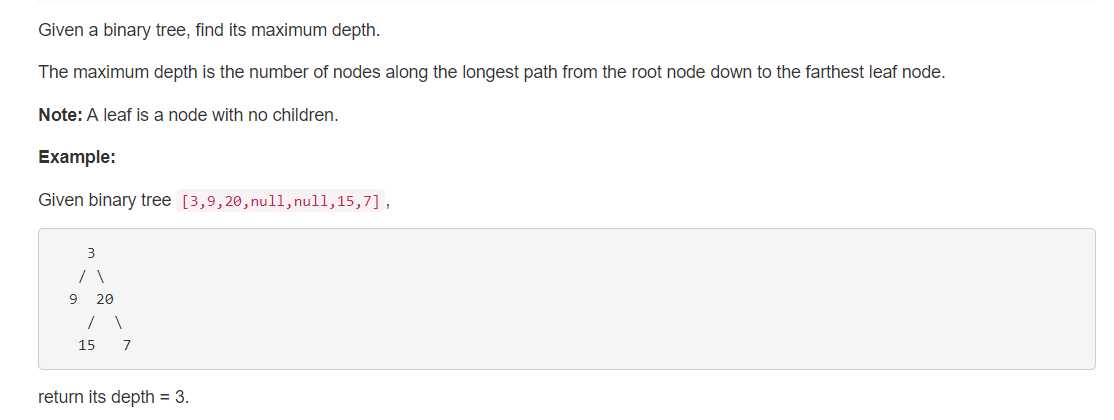
2、分析
给出一棵二叉树,输出其最大深度。
二、解答
1、思路:
方法一、
采用递归方式,输出其最大深度。
public int maxDepth(TreeNode root) { return getDepthHelper(root, 1); } private int getDepthHelper(TreeNode root, int depth) { if(root == null) return depth - 1; return Math.max(getDepthHelper(root.left, depth + 1), getDepthHelper(root.right, depth + 1)); }
方法二、
直接在此方法上递归。
public int maxDepth3(TreeNode root) { if(root == null) return 0; return 1 + Math.max(maxDepth(root.left), maxDepth(root.right)); }
方法三、
采用 BFS 广度优先遍历,用一变量记录深度。
public int maxDepth2(TreeNode root) { if(root == null) return 0; int depth = 0; Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.add(root); while(!queue.isEmpty()) { depth++; int size = queue.size(); while(size-- > 0) { if(queue.peek().left != null) queue.add(queue.peek().left); if(queue.peek().right != null) queue.add(queue.peek().right); queue.poll(); } } return depth; }
方法四、
利用 DFS 深度优先遍历方法;
采用两个栈,一个栈记录节点,另一个栈记录节点对应的深度,也采用一个变量记录最大深度。
public int maxDepth4(TreeNode root) { if(root == null) return 0; int max = 0; Stack<TreeNode> stack = new Stack<>(); Stack<Integer> value = new Stack<>(); stack.push(root); value.push(1); while(!stack.isEmpty()) { TreeNode node = stack.pop(); int tmp = value.pop(); max = Math.max(tmp, max); if(node.left != null) { stack.push(node.left); value.push(tmp+1); } if(node.right != null) { stack.push(node.right); value.push(tmp+1); } } return max; }
104. Maximum Depth of Binary Tree
标签:ISE 广度优先 linked 一个 com 记录 lis span 图片
原文地址:https://www.cnblogs.com/skillking/p/9733218.html