标签:lse ack inline text printf tin mem ssi using
题意:
一个矩形区域被分成 m*n 个单元编号为 (1, 1)至 (m, n),左上为 (1, 1),右下为(m, n)。给出P(k)i,j,其中 1 ≤ i ≤ m,1 ≤ j ≤ n,1 ≤ k ≤ 4,表示了 (i, j)到 (i+1, j),(i, j+1),(i-1, j),(i, j-1)的概率。一个骑士在 (1, 1),按照给定概率走,每步都于之前无关,问到达 (m, n)的期望步数。
解析;
很容易想到
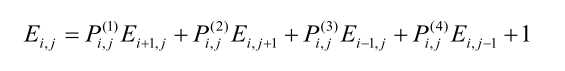
然后移项 写出行列式

图截自大佬题解
矩阵中 概率为负 1为正 是因为移项
然后从最后一行 向前化简化出上三角行列式就好了
在这个矩阵中,每行的系数都占据了(2m+1)的长度,且以f(i, j)为中心
因此我们在高斯消元的时候,只需要消除后m行中的m个系数
#include <iostream> #include <cstdio> #include <sstream> #include <cstring> #include <map> #include <cctype> #include <set> #include <vector> #include <stack> #include <queue> #include <algorithm> #include <cmath> #include <bitset> #define rap(i, a, n) for(int i=a; i<=n; i++) #define rep(i, a, n) for(int i=a; i<n; i++) #define lap(i, a, n) for(int i=n; i>=a; i--) #define lep(i, a, n) for(int i=n; i>a; i--) #define rd(a) scanf("%d", &a) #define rlld(a) scanf("%lld", &a) #define rc(a) scanf("%c", &a) #define rs(a) scanf("%s", a) #define pd(a) printf("%d\n", a); #define plld(a) printf("%lld\n", a); #define pc(a) printf("%c\n", a); #define ps(a) printf("%s\n", a); #define MOD 2018 #define LL long long #define ULL unsigned long long #define Pair pair<int, int> #define mem(a, b) memset(a, b, sizeof(a)) #define _ ios_base::sync_with_stdio(0),cin.tie(0) //freopen("1.txt", "r", stdin); using namespace std; const int maxn = 1700, INF = 0x7fffffff, LL_INF = 0x7fffffffffffffff; int n, m, tot; double p[maxn][maxn]; void gauss() { for(int i = tot, j = tot; i >= 1; i--, j--) { for(int k1 = i - 1; k1 >= i - m - 1 && k1 >= 1; k1--) { double f = p[k1][j] / p[i][j]; for(int k2 = j - 1; k2 >= j - m && k2 >= 1; k2--) { p[k1][k2] -= f * p[i][k2]; } p[k1][tot + 1] -= f * p[i][tot + 1]; } } } int main() { while(cin >> n >> m && n + m) { tot = n * m; double x; mem(p, 0); for(int k = 0; k < 4; k++) for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) { cin >> x; int pos = (i - 1) * m + j; if(k == 0) p[pos][pos] = -1; if(k == 0 && i < n) p[pos][pos + m] = x; else if(k == 1 && j < m) p[pos][pos + 1] = x; else if(k == 2 && i > 1) p[pos][pos - m] = x; else if(k == 3 && j > 1) p[pos][pos - 1] = x; } for(int i=1; i<=tot; i++) p[i][tot+1] = -1; p[tot][tot + 1] = 0; gauss(); printf("%.6f\n", p[1][tot + 1] / p[1][1]); } return 0; }
参考:
https://www.cnblogs.com/cjfdf/p/8467655.html
https://www.cnblogs.com/swm8023/archive/2012/09/01/2666303.html
First Knight UVALive - 4297(优化高斯消元解概率dp)
标签:lse ack inline text printf tin mem ssi using
原文地址:https://www.cnblogs.com/WTSRUVF/p/9733289.html