标签:正序 clu 代码 ima int code etc main 转移
这两天搞完01背包之后学习了完全背包这个完全背包是指物品数量无限,让自己来装考虑一下状态转移f[i][j]=max(f[i-1][j])尚未选择第i种物品,f[i][j]=max(f[i][j-w[i]+v[i]]);从第i键物品中选择一个显然状态是由不拿当前物品上一层的最优解和当前拿这个物品的最优解来进行比较从而进行转移。当然目标可以是maxf[n][j]或者是f[n][m]这两种都行只不过前者可以判断背包是否能被装满。
下面是二维的代码:

#include<ctime> #include<iostream> #include<cstdio> #include<algorithm> #include<cstdio> #include<iomanip> #include<map> #include<queue> #include<stack> #include<cstring> #include<string> #include<vector> using namespace std; inline long long read() { long long x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } const long long maxn=10001; long long f[maxn][maxn],w[maxn],v[maxn]; long long n,m; int main() { //freopen("1.in","r",stdin); m=read();n=read(); for(long long i=1;i<=n;i++) { v[i]=read();w[i]=read(); } for(long long i=1;i<=n;i++) for(long long j=1;j<=m;j++) { f[i][j]=max(f[i][j],f[i-1][j]); if(j>=w[i])f[i][j]=max(f[i][j],f[i][j-w[i]]+v[i]); } printf("%lld\n",f[n][m]); return 0; }
而一维的完全背包是那样子的,把f[j]=max(f[j-w[i]]+v[i]);正序来选择因为可以在刚刚更新过的第i件物品之上再进行更新这样的话就意味着一件物品有无数件了。不算是很懵了
下面是一维的代码:

#include<ctime> #include<iostream> #include<cstdio> #include<algorithm> #include<cstdio> #include<iomanip> #include<map> #include<queue> #include<stack> #include<cstring> #include<string> #include<vector> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } const int maxn=10001; int f[maxn],w[maxn],v[maxn]; int n,m; int main() { //freopen("1.in","r",stdin); m=read();n=read(); for(int i=1;i<=n;i++) { v[i]=read();w[i]=read(); } for(int i=1;i<=n;i++) { for(int j=w[i];j<=m;j++) { f[j]=max(f[j],f[j-w[i]]+v[i]); } } cout<<f[m]<<endl; return 0; }
又搞了一道01背包的方法数,这个还是比较简单的个人觉得方法数的话以下面的洛谷例题为例: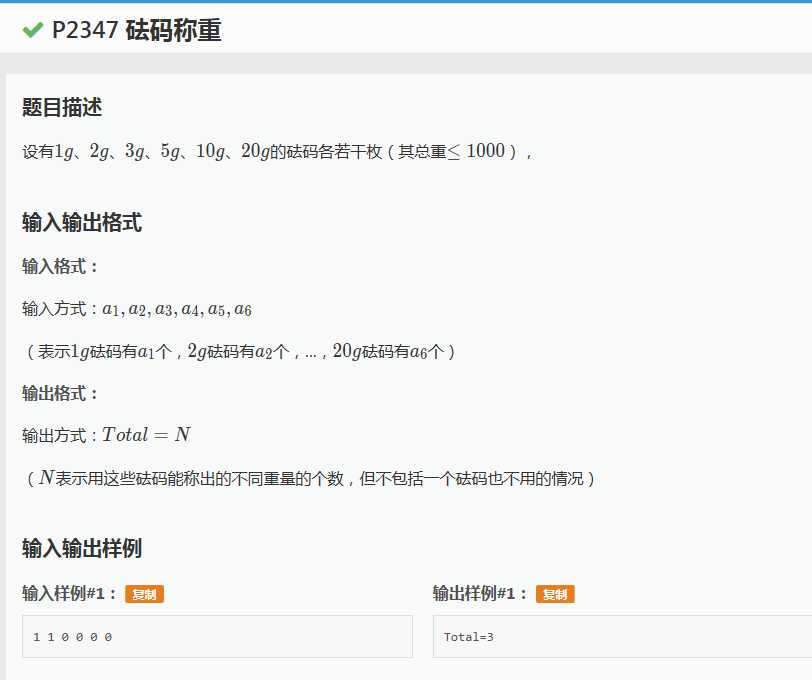
求出所有背包的数量,这样的话求助了学长,不会啊当时感觉特别困难做题没有举一反三的能力感觉自己还不行,灵性不够。这很显然是一道01背包的变形所以只要稍稍的把01背包的转移方程改一下即可,
f[j]=f[j]+f[j-w[i]];初始化f[0]=1;这样加上一些小细节这道题就可以被轻松a掉。
代码:

#include<ctime> #include<iostream> #include<cstdio> #include<algorithm> #include<cstdio> #include<iomanip> #include<map> #include<queue> #include<stack> #include<cstring> #include<string> #include<vector> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } const int maxn=1002; int a[7]={0,1,2,3,5,10,20}; int w[maxn],f[maxn],n=0,m=0,ans=0; int main() { //freopen("1.in","r",stdin); for(int i=1;i<=6;i++) { int x; x=read(); for(int j=1;j<=x;j++) { w[++n]=a[i]; m+=a[i]; } } f[0]=1; for(int i=1;i<=n;i++) { for(int j=m;j>=w[i];j--) { f[j]=f[j]+f[j-w[i]];//从i个数中来选和为j的有多少种方案 } } for(int i=1;i<=m;i++) { if(f[i]!=0)ans++; } printf("Total=%d\n",ans); return 0; }
标签:正序 clu 代码 ima int code etc main 转移
原文地址:https://www.cnblogs.com/chdy/p/9734254.html