波泼墨佛的特呢了

标签：表达式   递推   alt   变化   选择   线性   斐波那契数   循环结构   数据   

常量因子和算法复杂度：

对于算法的时间和空间性质，最重要的是其量级和趋势，这些是算法代价的主要部分，而代价函数的常量因此可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就可以认为它们的代价“差不多”。基于这样的考虑，人们提出描述算法性质的“大O记法”。

大O记法的严格定义：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c·g(n)，就说函数g是f的渐进函数(忽略常量因子)，记为f(n)=O(g(n))。易见，f(n)=O(g(n))说明在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束。把上述描述方式应用于算法的代价问题。假设存在函数g，使得算法A处理规模为n的问题实例所用的时间T(n)=O(g(n))，则称O(g(n))为算法A的渐进时间复杂度，简称时间复杂度。算法的空间复杂度S(n)的定义与此类似。

关于大O记法的几点说明。

首先，如果T(n)=O(g(n))，那么对于任何增长速度比g(n)更快的函数g‘(n)，显然也有T(n)=O(g‘(n))。这说明上述定义考虑的是算法复杂度的上限(应该说的是描述的是最糟糕的情况)。

其次，虽然可以选择任意合适的函数作为描述复杂性时使用的g(n)，但一组简单的单调函数已足以反映人们对基本算法复杂度的关注。(尽量简单)。在算法和数据结构领域，人们最常用的是一下这组渐进复杂度函数：

O(1)，常量复杂度

O(logn)，对数复杂度

O(n)，线性复杂度

O(n·logn)，

O(n2)，

O(n3)，

O(2?)，指数复杂度

在考虑量级时对数的底不是主要因素(可能差一个常量因子)，因此可以忽略。

按照上面的理论，如果算法的改进只是加快了常量倍，也就是说减少了复杂性函数中的常量因子，算法的复杂度没有变化。但是，在许多实际情况中，这种改进是有意义的。例如，需要3天时间算出明天的天气预报，与只需半天就能算出，算法的实际价值是截然不同的。

算法复杂度的意义

算法复杂度反过来决定了算法的可用性。

解决同一问题的不同算法

以斐波那契数列为例，定义如下：

F₀=F₁=1

F_n = F_n-1 + F_n-2，对于n>1

1 # 斐波那契数列，递归法
2 def fib(n):
3     if n <= 1:
4         return 1
5     return fib(n-1) + fib(n-2)
6 
7 print(fib(18))  # 4181

把参数n看作问题实例的规模，不难看出，计算F_n的时间代价(考虑求加法操作的次数)大致等于F_n-1 和 F_n-2的代价之和。这一情况说明，计算F_n的时间代价大致等于斐波那契数F_n的值。根据已有结论：

括号里的表达式大约等于1.618，所以计算F_n的时间代价按n值呈指数增长。对于较大的n，这一计算就需要很长很长时间。

使用递推方法，

 1 def fib(n):
 2     if n <= 1:
 3         return 1
 4     a = b = 1
 5     for i in range(1, n):  # n=2时只进行一次计算...
 6         c = b
 7         b = a + b
 8         a = c
 9     return b
10 
11 print(fib(18))  # 4181

书上是这么写的，

1 def fib(n):
2     f1 = f2 = 1
3     for i in range(1, n):  # n=2时只进行一次计算...，0、1对于range无效，所有可以把n=0或1的情况合并
4         f1, f2 = f2, f1+f2
5     return f2
6 
7 print(fib(18))  # 4181

使用这个算法计算F_n的值，循环前的工作只做一次，循环需要做n-1次。基本操作执行次数与n值呈某种线性关系。

这一例子说明，解决同一问题的不同算法，其计算复杂大的差异可以很大，甚至截然不同。当然，在实际工作中，可能两个算法可有所长，例如一个时间复杂大较低但空间复杂度较高，而另一个情况正好相反，这时，就需要做进一步的细致分析。

1.3.3 算法分析

算法分析的目的是推导出算法的复杂度，其中最主要的技术是构造和求解递归方程。

基本循环程序

这里只考虑时间复杂度，考虑最基本的循环程序，其中只有顺序组合、条件分支和循环结构。分析这种算法只需要几条基本计算规则：

0. 基本操作，认为其时间复杂度为O(1)。如果是函数调用，应该将其时间复杂度代入，参与整体时间复杂度的计算。

1. 加法规则(顺序复合)。如果算法(或所考虑算法片段)是两个部分(或多个部分)的顺序组合，其复杂性是这两部分(或多部分)的复杂性之和。以两个部分为例：

1

其中T₁(n)和T₂(n)分别为顺序复合的两个部分的时间复杂度。由于忽略了常量因子，加法等价于求最大值，取T₁(n)和T₂(n)中复杂度最高的一个。

2. 乘法规则(循环结构)。如果算法(或所考虑的算法片段)是一个循环，循环体将执行T₁(n)次，每次执行需要T₂(n)时间，那么：

1

3. 取最大规则(分支结构)。同顺序复合。如果算法(或所考虑的算法片段)是条件分支，两个分支的时间复杂性分别为T₁(n)和T₂(n)，则有：

实例，

1     for i in range(n):  # m1的每行
2         for j in range(n):  # 笛卡儿积，倒数第二层是m1的一行，m2的每列
3             x = 0.0
4             for k in range(n):  # 最里层是m1的行和m2的列一一对应
5                 x += m1[i][k] + m2[k][j]
6             m[i][j] = x

这个程序片段是一个两重循环(前两行)，循环体是一个顺序语句(3~6行)，其中还有一个内嵌的循环。根据上面的复杂性计算规则，可以做如下推导：

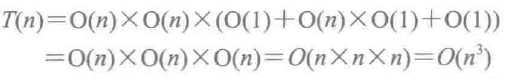
另一个实例，

求n阶方形矩阵的行列式。考虑两种不同算法。

行列式回忆，

波泼墨佛的特呢了

标签：表达式   递推   alt   变化   选择   线性   斐波那契数   循环结构   数据   

原文地址：https://www.cnblogs.com/yangxiaoling/p/9736552.html