标签：乘法逆元   技术   for   www.   技术分享   lan   blank   pre   解方程   

数论&数学从入门到放弃

组合数学

→组合数学常用公式

组合数：

将n个不同的球放入m个相同的盒子里的方案数

（从 n 个不同元素中每次取出 m 个不同元素，不管其顺序合成一组，称为从 n 个元素中不重复地选取 m 个元素的一个组合。所有这样的组合的种数称为组合数。）

递推公式：C（n，m）= C（n - 1，m - 1）+ C（n - 1，m）

（其它计算公式见组合数学常用公式）

推导方法：

• 若新的球独占一个盒子，则其它球占 m - 1 个盒子，共有 C（n - 1，m - 1）种方案
• 若新的球与其它球共用盒子，则分别与其它数在一个盒子，但有 n - 1 - m 个数是与其它数在同一集合中的，所以重复了 n - 1 - m 次，共有 C（n - 1，m - 1）* n / （n - 1 - m）= C（n - 1，m）种
  

只能向右、上走，从（0，0）到（n，m）的方案数

相当于在 n + m 个操作中选 n 个为上（横坐标加一）的方案数

即为 C（n + m，m）或 C（n + m，n）

从（0，0）到（n，m）不碰到 直线y = x + b 的方案数

计算公式：C（n + m，m）- C（n + m，n - b）

推导方法：

• 总方案数为 C（n + m，m）
• 将坐标系沿直线翻折，翻折后起点为（b，n - b），从翻折后的起点出发到达终点必会经过直线，且翻折后起点出发的路径都对应一条从原起点出发的路径

• 翻折后方案数 C（b + m + n - b，n - b）
• 所以不合法的方案数为 C（n + m，n - b）

 斯特林数

第一类斯特林数

n 个人坐 m 张圆桌的方案数

推导公式：s（n，m）= s（n - 1，m - 1）+ s（n - 1，m）*（n - 1）

推导方法：

• 新一个人单独做一张圆桌，方案数为 s（n - 1，m - 1）
• 新一个人与其它人共坐圆桌，他可以在任意一个人的左边坐下，所以对于之前的每一种方案都有 n - 1 种方案，根据乘法原理，方案数为 s（n - 1，m）*（n - 1）

第二类斯特林数

n 个球分成 m 个集合的方案数

推导公式：S（n，m）= S（n - 1，m - 1）+（n - 1，m）* m

推导方法：和上一种差不多

容斥原理

card表示集合的大小

card（a∪b）= card（a）+ card（b）- card（a∩b）

card（a∪b∪c）= card（a）+ card（b）+ card（c）- card（a∩b）- card（b∩c）-card（a∩c）+ card（a∩b∩c）

……

扩展欧几里得

用来求形如 a x + b y = gcd（a，b）的不定方程特解，且求出的解满足 |x|+|y| 最小

void exgcd(int a, int b, int &d, int &x, int &y) {
    b ? exgcd(b, a % b, d, y, x), y -= x * (a / b) : d = a, x = 1, y = 0;
}

欧拉定理

其中φ（n）为欧拉函数，即小于等于 n，且与 n 互质的数的个数。（a，n互质）

对于指数很大的情况，可以根据欧拉定理降幂

逆元

若满足

则称B在模A意义下的乘法逆元，逆元可以用来求带取模的除法

逆元的求法：

• 根据欧拉定理，快速幂求出：B = A^{P - 2} % P
• 解方程 P x + A y = 1，则 A y = 1 - P x，y Ξ 1 / A （mod P）
• 递推求逆元：

即 inv[i] = p -（p / i * inv[p % i]）% p

质数的求法

单个质数：

使用试除法，用小于等于sqrt（x）的数试除 x 若能除尽，则 x 为合数

bool prime(int x) {
	if(x == 2)return 1;
	if(x % 2 == 0 || x == 1)return 0;
	for(int i = (int)sqrt(x) | 1; i >= 3; i -= 2)
		if(x % i == 0)return 0;
	return 1;
}

求 1 ~ n之间的质数

使用筛法求质数

//复杂度很低的筛法
for(int i = 2; i <= n; i ++)
	if(! w[i]) {
		p[ ++cnt] = i;
		for(int j = 2; j <= i; j ++)w[i * j] = 1;
	}

//线性筛法
for(int i = 2; i <= n; i ++) {
	if(! w[i])p[ ++cnt] = i;
	for(int j = 1; j <= cnt && i * p[j] <= n; j ++) {
		w[i * p[j]] = 1;
		if(i % p[j] == 0)break;
	}
}

中国剩余定理

给出若干个方程，每一个都形如 x % Pi = ai，Pi互质且互不相同

BSGS算法

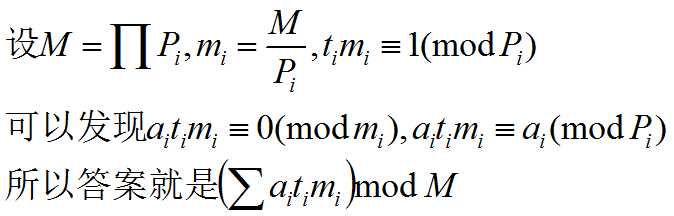
求形如 a^x Ξ b （mod P） 的方程的解

数论&数学

标签：乘法逆元   技术   for   www.   技术分享   lan   blank   pre   解方程   

原文地址：https://www.cnblogs.com/akakw1/p/9737555.html