参数估计（一）点估计之矩估计法（1）

时间：2018-10-04 11:22:17 阅读：330 评论：0 收藏：0 [点我收藏+]

在数理统计中，我们见过的总体X一般都是未知的。

即便根据以往的经验和数据，知道X服从那类分布，其数字特征（如数学期望、方差、矩）也是未知的.

这些未知的数字特征以及含在总体X中的未知数称为未知参数（简称参数）。

为了估计未知函数的真值或者所在区间，就要从总体X中抽取样本，然后用样本构造某种统计量，来估计未知参数的值或其范围。这种方法就叫做参数估计。

点估计就是根据样本构造的一个统计量（称为估计量）来估计总体的真实参数值（参数真值）。比如辛钦大数定理，设X1,X2,?是独立同分布的随机变量序列，且它们的期望值存在，记为E(Xi)=μ(i=1,2,?)，则对于任意的?>0，有

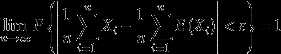
作为a的近似值，而且随着n的增大，与a之间的误差会越来越小。

技术分享图片

　　　　估计量和估计值统称为估计

构造的统计量称为点估计量，得到的估计值称为点估计值。所以对于不同的样本所得到的估计值也是不一样的。

我们用样本构造的统计量是否能作为未知参数的估计量，这需要一定的合理性和理论依据。

下面介绍两种常用的构造统计量的方法：

（1）矩估计法

（2）最大似然估计法

矩估计法

矩估计法的思想　　　　　　矩估计法的思想是用样本的各阶矩去近似代替总体的各阶矩。

原文地址：https://www.cnblogs.com/kitor/p/9740476.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

周排行