标签:提升 http 图片 群集 自动 优化问题 ppi png 共享
NSGA-II入门C1
参考文献1
参考文献2
白话多目标
多目标中的目标是个瓦特?
多目标即是优化问题中的优化目标在3个及以上,一般这些优化的目标都存在着矛盾,例如:我要买一个又便宜又漂亮又性能好的车的时候,价格,外观, 性能 这就是一个典型的多目标问题,我们必须在商品的价格,外观和性能上做出取舍,毕竟外观漂亮性能强劲的车型往往意味着高的价格。
多目标中的支配是个瓦特?
我们经常听说 支配与非支配解集 ,那么什么叫做支配,什么叫做非支配呢?还是上面汽车的例子,如果汽车A价格30万,外观A等,性能A等;汽车B价格40万,外观A-等,性能A-等,就说汽车A支配了汽车B。如果有一辆汽车C价格20万,外观B等,性能B等,相较于汽车A,虽然C的外观和性能都比汽车A要差,但是其价格上比汽车A要低,从价格这个评价标准上来看,汽车C是要优于汽车A的,所以说汽车C和汽车A是属于一个非支配的关系。即 当A所有目标都优于B时,就说A支配了B,否则A和B就是一个非支配的关系 ,而在NSGA-II中,种群中所有不被任何其他解支配的解构成了非支配前沿(Pareto最优解)
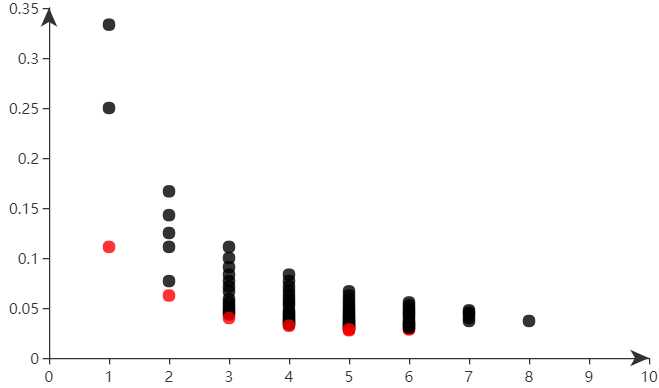
多目标遗传算法与遗传算法的区别-选择的方法不同
多目标遗传算法与遗传算法的联系-交叉变异的方法相同
- 遗传算法中和多目标遗传算法中最大的不同在于 选择 的过程,遗传算法中通过适应度函数进行种群中个体的选择,而多目标遗传算法中根据 非支配的Rank值和拥挤度进行排序 选择保留的个体。
- 对于Rank值,首先我们将解集中的 所有不能被任何其他的解支配的解集 (即最厉害最牛的解)挑出来设为Rank0,然后将这些解从解集中排除,考虑剩下所有解中 所有不能被任何其他的解支配的解集 挑出来设为Rank1,...通过支配关系将解集中所有的解进行排序,得到所有解的等级。我们认为 Rank值越小的解越好。
- 在选择的过程中我们设定 每次迭代种群中个体的数量N是定值 ,而每次挑选时,先挑选表现最好的解--即Rank0的解,接着是Rank1,Rank2,Rank3...,但是我们总会出现\[\sum^{n-1}_{i=0}Rank_i>N\] 而 \[\sum^{n}_{i=0}Rank_i<N\] 的情况,为了判定同一个Rank层的解的好坏,设置 拥挤度 作为同Rank非支配解集中解的评价标准。
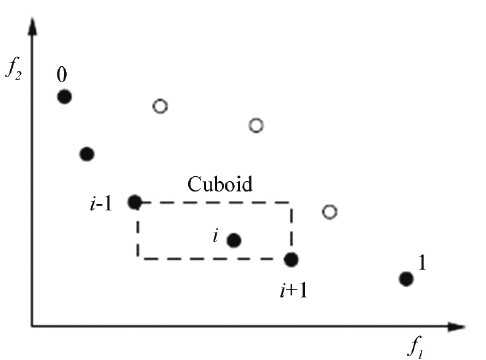
- 遗传算法有自动收敛的性质,所以为了保证解的多样性,我们往往希望同一Rank层中的解能够相互分开,所以设置了 拥挤度 这个概念,认为 解之间距离开的解比解之间距离小的解更好 拥挤距离排序用于保持解的多样性。 每个个体的拥挤距离是通过计算与其相邻的两个个体在每个子目标函数上的距离差之和来求取,即下图中虚线四边形的长和宽之和
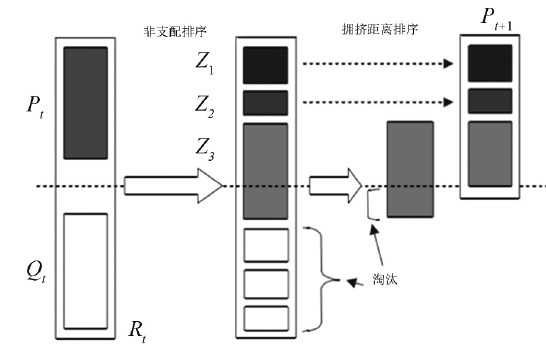
每个父代\(P_t\)都会通过 交叉和变异 (其中多目标遗传算法中的交叉和变异与传统遗传算法中的交叉和变异没有区别) 生成子代\(Q_t\) ,父代和子代的所有个体集合称为 \(R_t\) ,先通过 非支配排序 选出\(R_t\)中的合适个体,再通过 拥挤度排序 选出同一Rank层中的个体,使新的种群集合 \(P_{t+1}\) 的个体数目为N。 这一过程常常会使用以下两种图进行表示:
学术多目标
NSGA-II算法的今生前世
在遗传算法在解决多目标优化遇到瓶颈时,许多学者花费了不少时间和精力在多目标优化的遗传算法上,Goldberg首先将Pareto最优解的概念与适应度值概念相关联,即将Pareto非支配排序分层的概念与适应度联系,排序的层次低,则其分层中个体的适应度值较高,使算法能够朝着Pareto最优前沿进化,最终输出Pareto最优解集。在提出此概念后,学者们陆续提出了一系列多目标遗传算法,如SPGA、NPGA、FFGA、NSGA等等。但是最能代表Goldberg思想的算法是基于非支配排序的遗传算法,即NSGA(Non—dominated Sorting Genetic Algorithm)。
科学家Srinivas和Deb在前人研究基础上,于1994年首先提出了非支配排序遗传算法的概念。其算法最主要的思想是 将所有的个体进行分层,并且对每个个体都设置个体虚拟适应度值同一层中的每个个体虚拟适应度值相同,层级数越低,其适应度值越高,遗传到下一代的概率也就越大。为了使得到的结果沿Pareto前沿均匀分布,就需要保证非支配层中个体保持多样性,为了保持非支配层中个体多样性,Srinivas等人采用了共享函数法。
采用非支配排序的遗传算法在多目标优化中得到了广泛应用,但是,随着其使用越广泛,其算法也暴露出了一些缺陷。 首先,NSGA算法的时间复杂度高,为\(O(mN^3)\),m代表目标数,N表示种群规模大小,当种群数目过多时,其排序过程必将耗费更多时间,降低了搜索效率。再者,NSGA算法没有考虑精英策略,精英策略能提高算法的计算速度,也能将优秀个体保存下来。更为重要的一点是,其共享半径参数是人为设定的,而共享半径设置不合理,将对计算结果产生非常大的影响。
为了克服非支配排序遗传算法的以上弊端,Deb等学者于2000年对NSGA算法进行了改进,提出了 基于快速非支配排序的遗传算法NSGA-II,相比NSGA来说,NSGA-II有如下不同点 :
- 计算复杂度 在NSGA计算中,其排序的复杂程度为\(O(mN^3)\)(m代表目标函数个数,N表示种群规模),而采用NSGA—II算法,其计算复杂程度将为\(O(mN^2)\),计算效率得到了提升。
- 算法中加入了精英策略 其实现思想是:父代个体通过遗传操作产生予代个体后,选择操作选择的个体数N需要从父代和子代个体竞争,从中选出最好的,这样做的目的就是能将最优秀的个体保存下来。
- 相比NSGA算法提出的共享半径,NSGA—II采用了拥挤度的概念 在同一非支配层中,通过判断个体周围的拥挤程度,改善同一支配层面的种群多样性,不需要设定比较“敏感”的共享半径参数,对提高算法效率和保持种群多样性上优于NSGA算法。
NSGA-II 该算法求得的 Pareto 最优解分布均匀,收敛性和鲁棒性好,具有良好的优化效果,是求解多目标优化问题的一种新思路
非支配排序
- 时间复杂度 m 个个体和种群中的其他个体进行支配关系比较,是否支配其他全部个体,复杂度为O(mN);循环进行直到等级1 中的非支配个体全部被搜索到,复杂度为\(O(mN^2)\);最坏的情况下,有N个等 级,每个等级只存在一个解,复杂度为\(O(mN^3)\)
- 算法流程 NSGA—II排序时需要设定两个参数用\(n_i\)表示种群中所有个体中支配个体i的数目,\(S_i\)表示种群中个体被个体i支配的个体集合。NSGA-II对种群个体进行非支配排序的步骤如下:
- 找出种群中非支配解的个体,即\(n_i=0\)的个体,将非支配个体放入集合F1中。
- 对于F1中的每个个体,找出集合中每个个体所支配个体集合\(S_i\),对\(S_i\)中的个体l,对\(n_l\)进行减1操作,令\(n_l = n_l-1\) ,若\(n_l\)大小为0,则将此个体存放在集合H中。
- 定义集合F1为第一层非支配集合,并为F1中每个个体标记相同的非支配序列\(i_{rank}\)。
- 对集合H中的个体,按照以上步骤1、步骤2和步骤3操作,直至将所有个体分层。
拥挤度排序
- 目的 同一层非支配个体集合中,为了保证解的个体能均匀分配在Pareto前沿,就需要使同一层中的非支配个体具有多样性,否则,个体都在某一处“扎堆”,将无法得到Pareto最优解集。NSGA—II采用了拥挤度策略,即计算同一非支配层级中某给定个体周围其他个体的密度。
- 每个个体的拥挤距离是通过计算与其相邻的两个个体在每个子目标函数上的距离差之和来求取。\[D_i=(f_{i+1,1}-f_{i-1},1)+(f_{i-1,2}-f_{i+1,2})\] ,即下图中虚线四边形的长和宽之和。

NSGA-II排序算法
- 当每个个体拥有这两个属性,就可以通过这两个属性判定任意两个个体的支配关系。当两个体没有处在同一非支配层级时,通过判断\(i_{rank}\)大小,确定个体优劣,\(i_{rank}\)值小的个体比\(i_{rank}\)大的个体更优;当两随机个体处于同一非支配层级时,依据个体拥挤度判定个体孰优孰劣,个体拥挤度大的比个体拥挤度小的个体更优
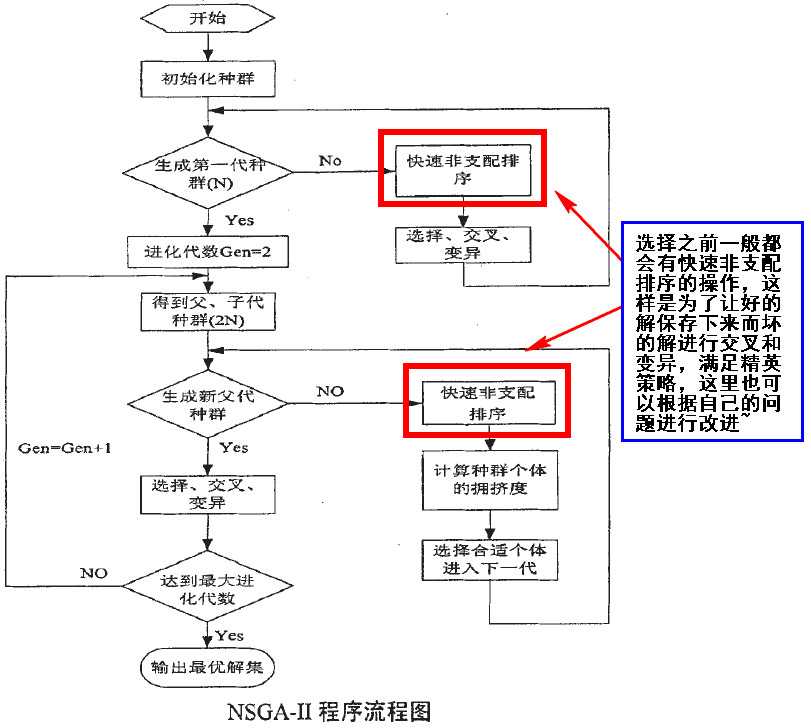
NSGA-II算法流程
NSGA-II算法流程-达到一定进化代数停止
首先种群初始化,通过快速非支配排序、选择、交叉以及变异操作后得到初始种群,种群中个体数为N;将父代种群和子代种群合并,再通过排序、拥挤度计算得出下一代种群个体;得出新一代种群后根据遗传操作继续产生下一代,如此反复,直到达到进化最大代数停止。

NSGA-II算法流程-算法收敛停止
- 创造一个初始父代种群 \(P_0\) 使用交叉和变异操作产生子代种群 \(Q_0\)
- 对 \(P_0\) h和 \(Q_0\) 组成的整体 \(R_0\) 进行非支配排序,构造所有不同等级的非支配解集 \(Z_1,Z_2,Z_3 ...\)
- 对分好等级的非支配解集进行拥挤距离排序,根据适应度高低得到前 N 个解,构成下一次迭代的父代种群 \(P_1\)
- 重复上述 3 个步骤,直到结果收敛

NSGA-II入门C1
标签:提升 http 图片 群集 自动 优化问题 ppi png 共享
原文地址:https://www.cnblogs.com/cloud-ken/p/9741962.html






