标签:close ret col def 从后往前 \n gcd pow sizeof
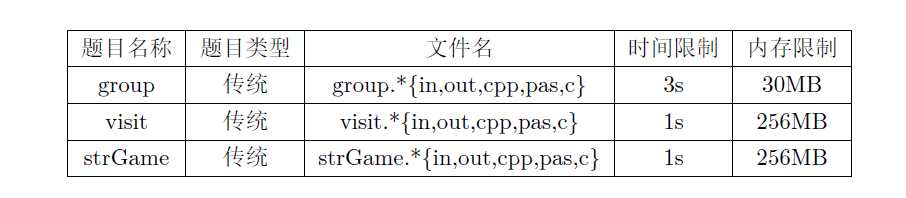



第一题:
轮廓线DP,从后往前存;复杂度R*C*2^16;
学习了一波std的写法,非常优美;

#include<bits/stdc++.h> using namespace std; const int M = (1<<16) + 1; int dp[2][M], cnt[M], len[130]; char sc[130][20]; inline int bit(int x){ if(!x) return 0; return bit(x>>1) + (x&1); } int main(){ freopen("group.in","r",stdin); freopen("group.out","w",stdout); int n, m; scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++){ scanf("%s", sc[i] + 1); len[i] = strlen(sc[i] + 1); } for(int s = 0; s < (1<<m); s++) cnt[s] = bit(s); int u = 1; for(int i = 1; i <= m; i++) sc[0][i] = ‘$‘; for(int i = 0; i < n*m; i++){ u ^= 1; memset(dp[u^1], 0, sizeof(dp[u^1])); int row = i/m, now = i%m; for(int s = 0; s < (1<<m); s++){ int nxt = s>>(m-now), lst = s^(nxt<<(m-now)); int lstnum = cnt[lst], nxtnum = cnt[nxt]; if(nxtnum > len[row+1] || nxtnum + m - now < len[row+1] || lstnum > len[row] || lstnum + now < len[row])continue; if(nxtnum < len[row+1]){ int tmp = 0; if((s&1) && (sc[row+1][nxtnum+1] == sc[row][len[row]-lstnum+1])) tmp += 2; if((s&(1<<(m-1))) && (sc[row+1][nxtnum] == sc[row+1][nxtnum+1])) tmp += 2; int &t = dp[u^1][(s>>1) | (1<<(m-1))]; t = max(t, dp[u][s] + tmp); } int &t = dp[u^1][s>>1]; t = max(t, dp[u][s]); //printf("%d %d %d %d\n",row, now, s, dp[u][s]); } } int ret = 0; for(int s = 0; s < (1<<m); s++)ret = max(ret, dp[(n*m)&1][s]); printf("%d\n", ret); }
第二题:
组合数,枚举向左走了多少步, 那么向右向下向上的步数都确定了,然后在T步中分配这些位置就好了;
C(T, lf) * C(T - lf, rg) * C(T - lf - rg, up);
60:

#include<bits/stdc++.h> using namespace std; #define ll long long const int M = 3e5; ll mod, fac[M], vfac[M]; int C[105][105]; inline int moc (int a){return a >= mod ? a - mod : a;} ll exgcd(ll a, ll b, ll &x, ll &y){ if(!b){x=1;y=0;} else { ll x0, y0; exgcd(b, a%b, x0, y0); x = y0; y = x0 - (a/b)*y0; } } inline ll ni(ll a){ ll x, y; exgcd(a, mod, x, y); return (x%mod + mod)%mod; } void init(int T){ int ret = T; fac[0] = vfac[0] = 1; for(int i=1;i<=ret;i++) { fac[i]=fac[i-1]*(ll)i%mod, vfac[i]=ni(fac[i]); } } void init2(int T){ int ret = T; for(int i=0;i<=ret;i++) for(int j=0;j<=i;j++) if(j==0||i==j)C[i][j]=1; else C[i][j] = moc(C[i-1][j-1] + C[i-1][j]); } int main(){ freopen("visit.in","r",stdin); freopen("visit.out","w",stdout); int T; scanf("%d%lld", &T, &mod); if(T <= 100){ init2(T); int n, m, ans = 0; scanf("%d%d", &n, &m); if(n < 0) n = -n; if(m < 0) m = -m; int res = T - n - m; if(res < 0 || res & 1)return !puts("0"); res/=2; for(int i=0;i<=res;i++){ int a1 = C[T][i+n]; int a2 = C[T-i-n][i]; int a3 = C[T-i-n-i][res-i]; ans = (ans + a1 * a2 % mod * a3 % mod) % mod; } printf("%d\n", ans); } else { init(T); int n, m;ll ans = 0; scanf("%d%d", &n, &m); if(n < 0) n = -n; if(m < 0) m = -m; int res = T - n - m; if(res < 0 || res & 1)return !puts("0"); res/=2; for(int i=0;i<=res;i++){ ll a1 = fac[T] * vfac[i+n] % mod * vfac[T - (i+n)] % mod; ll a2 = fac[T-i-n] * vfac[i] % mod * vfac[T-i-n-i] % mod; ll a3 = fac[T-i-n-i] * vfac[res-i] % mod * vfac[T-i-n-i-(res-i)]% mod; ans = (ans + a1 * a2 % mod * a3 % mod) % mod; } printf("%lld\n", ans); } }
100:(std)(对于模数不是质数的,有些数就没有拟元了,要用中国剩余定理)

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int MAXN=100005 ; int T, MOD, n, m ; int fac[50] , pw[50], fcnt ; long long jc[50][MAXN] ; int num[50][MAXN] ; long long powMod(long long a,long long b,long long c){ long long ret=1; while(b){ if(b&1) ret=ret*a%c ; a=a*a%c ; b>>=1 ; } return ret; } void preDo(){ for(int i=1;i<=fcnt;++i){ jc[i][0]=1 ; for(int j=1;j<=T;++j){ num[i][j]=num[i][j-1] ; int t=j ; while(t%fac[i]==0){ t/=fac[i] ; num[i][j]++ ; } jc[i][j]=jc[i][j-1]*t%fac[i] ; } } } long long C(long long a, long long b, int t){ int c=fac[t] ; if(num[t][a]-num[t][b]-num[t][a-b]>0) return 0 ; return jc[t][a]*powMod(jc[t][b],c-2,c)%c*powMod(jc[t][a-b],c-2,c)%c ; } long long C(long long a,long long b){ long long ans=0 ; for(int i=1;i<=fcnt;++i){ if(pw[i]!=1) cout << "WAAAA" ; long long tm=MOD/fac[i] ; ans += C(a,b,i)*tm%MOD*powMod(tm,fac[i]-2,fac[i])%MOD ; while(ans>=MOD) ans-=MOD ; } return ans ; } int main(){ freopen("visit.in","r",stdin) ; freopen("visit.out","w",stdout) ; long long ans=0 ; cin >> T >> MOD >> n >> m ; int tmp=MOD ; for(int i=2;i<=tmp;++i){ if(tmp%i==0){ fac[++fcnt]=i ; while(tmp%i==0) tmp/=i, pw[fcnt]++ ; } if(i*i>tmp && i<tmp) i=tmp-1 ; } preDo() ; for(int rr=0;rr<=T;++rr){ int ll=rr-n ; if(ll<0 || (T-ll-rr+m)&1) continue ; int uu = (T-ll-rr+m)/2 , dd = uu-m ; if(uu<0 || dd<0) continue ; ans += C(T,uu)*C(T-uu,dd)%MOD*C(T-uu-dd,ll)%MOD ; while(ans>=MOD) ans-=MOD ; } cout << ans << ‘\n‘ ; return 0 ; }
第三题:
博弈论,前缀性质想到建Trie树,怎么在上面跑博弈论呢?
如果只有一轮我们就看他是必赢或必输就好了,但是有多盘,可以选择战略性这盘输或赢;
我们保存这个节点是否有选择赢或输的权利;
从叶子节点出发,只有选择输的权利;
从非叶子节点出发,只要有一个儿子没有选择输的权利,他就有选择输的权利;只要有一个儿子没有选择赢的权利,他就有选择赢的权利;
考虑根节点,如果他有选择赢和输的权利,它可以前面一直输,最后赢;如果他只有选择赢的权利,就看K的奇偶性;其他情况都是后手必胜

#include<bits/stdc++.h> using namespace std; const int M = 1e6; int ch[M][27], tot; bool lose[M], win[M]; void insert(char *s){ int len = strlen(s); int now = 0; for(int i = 0; i < len; i++){ int t = s[i] - ‘a‘; if(!ch[now][t]) ch[now][t] = ++tot; now = ch[now][t] ; } } void dfs(int u){ int child = 0; for(int i = 0; i <= 25; i++) if(ch[u][i]){ int son = ch[u][i]; dfs(son); child++; if(!win[son]) win[u] = 1; if(!lose[son]) lose[u] = 1; } if(!child){ lose[u] = 1; } } void init(){ memset(win, 0, sizeof(win)); memset(lose, 0, sizeof(lose)); memset(ch, 0, sizeof(ch)); tot = 0; } int main(){ freopen("strGame.in","r",stdin); freopen("strGame.out","w",stdout); int T, n, k; char s[100005]; scanf("%d", &T); while(T--){ scanf("%d%d",&n,&k); init(); for(int i=1;i<=n;i++){ scanf("%s", s); insert(s); } dfs(0); if(win[0] && lose[0])puts("Pure"); else if(win[0]) (k%2) ? puts("Pure") : puts("Dirty"); else puts("Dirty"); } }
标签:close ret col def 从后往前 \n gcd pow sizeof
原文地址:https://www.cnblogs.com/EdSheeran/p/9742681.html