标签：size   info   总结   概率   nbsp   amp   9.png   com   enter   

二维Gibbs Sampling算法

Gibbs Sampling是高维概率分布的MCMC采样方法。二维场景下，状态(x, y)转移到(x’, y’)，可以分为三种场景

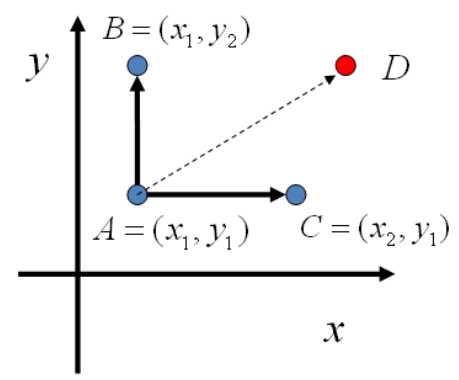
（1）平行于y轴转移，如上图中从状态A转移到状态B。

（2）平行于x轴转移，如上图中从状态A转移到状态C。

（3）其他情况转移，如上图从状态A转移到状态D。

对于上述三种情况，我们构造细致平稳条件

（1）A -> B

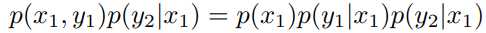
B –> A

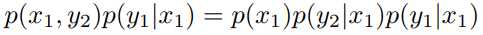
显然有

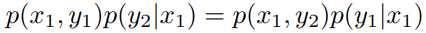
即

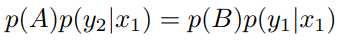
我们令转移矩阵中x = x1轴上的状态转移概率为p(y|x1)，则场景一天然满足细致平稳条件。

（2）同理，我们令转移矩阵中y = y1轴上的状态转移概率为p(x|y1)，则场景二天然满足细致平稳条件。即

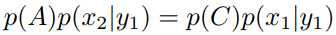
（3）对于场景三，我们不允许其转移。即

p(A) * 0 = p(D) * 0

实际上，从状态A转移到状态D可以通过一次场景一转移和一次场景二转移得到。所以即使规定A到D的转移概率为0，也满足A到D可以经过有限次转移达到。

总结一下，在二维概率分布的场景下，转移矩阵按照如下方式构造，马氏链即可达到指定的二维联合概率分布平稳状态

二维Gibbs Sampling算法

n维Gibbs Sampling算法

n维场景的考虑，与二维概率分布考虑一致：只允许状态沿着某一个维度平行转移，其他情况下状态转移概率为0。

（1）平行于y维转移

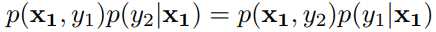
（2）其他情况转移

p(X1) * 0 = p(X2) * 0

n维Gibbs Sampling算法

参考：《LDA数学八卦》

Gibbs Sampling深入理解

标签：size   info   总结   概率   nbsp   amp   9.png   com   enter   

原文地址：https://www.cnblogs.com/coshaho/p/9743924.html