标签:不用 size 第一条 src png def return == 情况
题意:有一个未知的边权为$1$的图,给定所有点到$1$的最短路$a_i$和到$2$的最短路$b_i$,问是否存在这样的图,如果存在,问图中最少有多少条边
先考虑$a_i$,有$a_1=0,a_i\neq0(i\neq1)$,对于一条边$(x,y)$有$|a_x-a_y|\leq1$,对于任意$x\neq1$,存在$(x,y)$使得$a_x-1=a_y$,对$b_i$也有类似的约束
所以,我们将点$i$作为$(a_i,b_i)$画在平面上,那么至少要有两条边:第一条连到$(a_i-1,b_i-1)$或$(a_i-1,b_i)$或$(a_i-1,b_i+1)$,第二条连到$(a_i-1,b_i-1)$或$(a_i,b_i-1)$或$(a_i+1,b_i-1)$,如果这时找不到可以连边的点,那么就无解了(点$1$不用连第一种边,点$2$不用连第二种边)
如果可以连,那么我们构造出了一个有$2n-2$条边的图,显然这个图是满足条件的
但我们要最小化图中边数,所以考虑寻找尽可能多的可以共用的边
以下我们将第一种边称为$a$边,第二种边称为$b$边,共用边只可能是两种情况:1.对于点$i$,存在$(a_i-1,b_i-1)$,此时$i$的$a$边和$b$边可以共用;2.存在$i,j$使得$a_i-1=a_j,b_i+1=b_j$,此时$i$的$a$边可以和$j$的$b$边共用
我们把这$2n-2$条边看成点,如果两条边可以共用,在代表它们的点之间连一条边,求最大匹配即可,虽然是一般图,但注意到只有那些满足$a_i+b_i$相等的点$i$引出的边才可能共用,所以建出来的图是这样的(图来自官方题解)
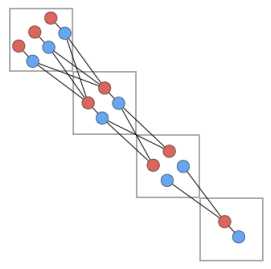
图中框代表某个坐标$(a_i,b_i)$上的点,红点代表$b$边,蓝点代表$a$边,如果方框内有连边说明存在$(a_i-1,b_i-1)$
这种分层图可以从左上往右下贪心选边求最大匹配,实现时只需维护每个坐标的未匹配点个数即可
总时间复杂度为$O(n\log n)$,感觉这题还是不错的
#include<stdio.h>
#include<map>
using namespace std;
map<int,map<int,int> >mp,vis;
int a[100010],b[100010];
bool ex(int x,int y){
return mp.count(x)&&mp[x].count(y);
}
int main(){
int n,i,j,s,las,now;
scanf("%d",&n);
#define wa {puts("-1");return 0;}
for(i=1;i<=n;i++){
scanf("%d%d",a+i,b+i);
if(i!=1&&a[i]==0)wa
if(i!=2&&b[i]==0)wa
mp[a[i]][b[i]]++;
}
for(i=1;i<=n;i++){
if(i!=2){
if(!(ex(a[i]-1,b[i]-1)||ex(a[i],b[i]-1)||ex(a[i]+1,b[i]-1)))wa
}
if(i!=1){
if(!(ex(a[i]-1,b[i]+1)||ex(a[i]-1,b[i])||ex(a[i]-1,b[i]-1)))wa
}
}
s=0;
for(i=1;i<=n;i++){
if(!ex(a[i]-1,b[i]+1)&&!vis[a[i]][b[i]]){
vis[a[i]][b[i]]=1;
las=0;
for(j=0;ex(a[i]+j,b[i]-j);j++){
now=mp[a[i]+j][b[i]-j];
s+=min(las,now);
now-=min(las,now);
if(ex(a[i]+j-1,b[i]-j-1)){
s+=now;
now=min(las,mp[a[i]+j][b[i]-j]);
}else
now=mp[a[i]+j][b[i]-j];
las=now;
}
}
}
printf("%d",2*n-2-s);
}
[CODE FESTIVAL 2016 Exhibition A]Distance Pairs
标签:不用 size 第一条 src png def return == 情况
原文地址:https://www.cnblogs.com/jefflyy/p/9744260.html