标签：水题   实现   难点   bubuko   through   标记   san   简单图   邻接表   

◆HDU-5215◆ Cycle

国庆节集训的第三天……讲图论，心情愉快……刷了一堆水题，不过也刷了一些有意思的题

+传送门+ HDU

? 题目

给出一个无向图（无自环，无重边），求该无向图中是否存在奇环、偶环。

多组数据，每组数据第一行为n,m表示点和边的数量，接下来m行每行描述一条边。

对于每组数据，输出两行，第一行输出是否存在奇环，第二行输出是否存在偶环。

? 解析

因为是一个简单图，这道题就简单了很多。

（1）判断奇环

有一类图是不包含奇数环的——二分图，反过来也是这样——二分图是不包含奇数环的图，所以不是二分图的图就一定包含奇数图。我们就只需要判断原图是否是二分图即可~ 黑白染色判断二分图就可以了。

（2）判断偶环

重点和难点基本上就在这儿了。

我们知道对于每一个连通块我们可以生成一棵DFS树，树上存在树边和返祖边（对这方面知识不熟的reader们建议先学了DFS树再看）。而一些树边和一条返祖边就会构成一个环——如果一条返祖边的两端点在DFS树上的路径距离为奇数，那么加上返祖边就形成了一个偶环。

当然形成偶环也不止这一个情况——看下面两种：

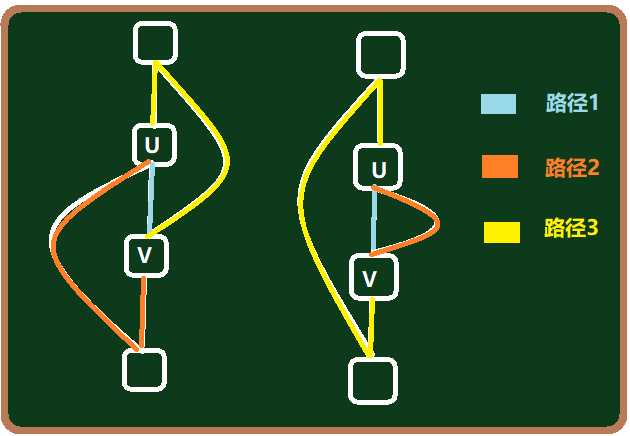
所以总结一下——另一种情况，存在两组点(a,b)(c,d)，a与b、c与d在树上的距离都为偶数（如果为奇数的话加上一条返祖边就可以直接形成偶数环了），且a->b和c->d的路径相交（点相交即可），那么就存在偶环，即路径2+路径3。

如上图所示，两个返祖边的端点之间的树边有交集 路径1 ，所以它们可以形成偶数环。

（3）具体实现

听起来像需要2次DFS，但是其实只需要一次——DFS可以同时实现判断二分图和树边、返祖边。

由于可能存在多个连通块，所以依次枚举起点u，如果u没有访问过，则从u开始遍历连通块，同时将u先染色。

若当前在节点u，则通过邻接表遍历u的儿子v，注意枚举v时要将v到达u的父亲的情况舍去。若发现v没有被遍历过，则将v染色后继续从v点遍历；否则经过了一条返祖边，判断v的颜色：

① col[v] ≠ col[u] ： 则u->v的路径为奇数，二分图染色成功，存在偶环；

② col[v] = col[u] ： 则u->v的理解为偶数，存在奇环；遍历u->v的路径，如果路径上有点已经被打上标记，则说明有另外一条返祖边的两端点之间的路径与当前u->v的路径相交，存在偶环，否则将 u->v 的路径上的点全部打上标记；

输出即可。

? 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=int(1e5);
int n,m;
vector<int> lnk[N+5];
int col[N+5],fa[N+5];
bool cov[N+5];
bool odd,eve;
void DFS(int u,int pre){
	for(int i=0;i<lnk[u].size();i++){
		int v=lnk[u][i];
		if(v==pre) continue;
		if(col[v]==-1){
			col[v]=!col[u];
			fa[v]=u;
			DFS(v,u);
		}
		else{
			if(col[v]==col[u]){
				odd=true;
				int pnt=u;
				while(!eve){
					if(cov[pnt]) eve=true;
					cov[pnt]=true;
					pnt=fa[pnt];
					if(pnt==v || pnt==-1) break;
				}
			}
			else eve=true;
		}
	}
}
void Clear(){
	memset(cov,false,sizeof cov);
	memset(fa,-1,sizeof fa);
	memset(lnk,0,sizeof lnk);
	memset(col,-1,sizeof col);
	odd=eve=false;
}
int main(){
	int T;scanf("%d",&T);
	while(T--){
		Clear();
		scanf("%d%d",&n,&m);
		for(int i=0;i<m;i++){
			int u,v;
			scanf("%d%d",&u,&v);
			lnk[u].push_back(v);
			lnk[v].push_back(u);
		}
		for(int i=1;i<=n;i++)
			if(col[i]==-1){
				col[i]=1;
				DFS(i,-1);
			}
		printf("%s\n%s\n",odd?"YES":"NO",eve?"YES":"NO");
	}
	return 0;
}

【杂题总汇】HDU-5215 Cycle

标签：水题   实现   难点   bubuko   through   标记   san   简单图   邻接表   

原文地址：https://www.cnblogs.com/LuckyGlass-blog/p/9740772.html