标签:rac red sqrt alt 逻辑 .com gif https 构造
1、直接给出;
如函数\(f(x)\)在某区间\(D\)上是奇函数。
2、以定义式给出;
如\(\forall x \in D,f(-x)= - f(x)\),则它是奇函数。如函数\(f(x)=x^3\),
3、定义的变形式给出;
如\(\forall x \in D,f(-x)+ f(x)=0\),\(\cfrac{f(-x)}{f(x)}=\pm 1(f(x)\neq0)\).
【应用①】
比如函数\(f(x)=ln(\sqrt{x^2+1}-x)\),
则可知\(f(-x)=ln(\sqrt{x^2+1}+x)\),
即\(f(x)+f(-x)=ln1=0\),即函数\(f(x)\)为奇函数;
那么函数\(f(x)=ln(\sqrt{x^2+1}-x)+1\)呢?
同理可得,\(f(x)+f(-x)=2\),
即函数\(f(x)\)关于点\((0,1)\)对称。
【应用②】
比如函数\(g(x)=lg(\sqrt{sin^2x+1}+sinx)\),
则可知\(g(-x)=lg(\sqrt{sin^2x+1}-sinx)\),
即\(g(x)+g(-x)=lg1=0\),即函数\(g(x)\)为奇函数;
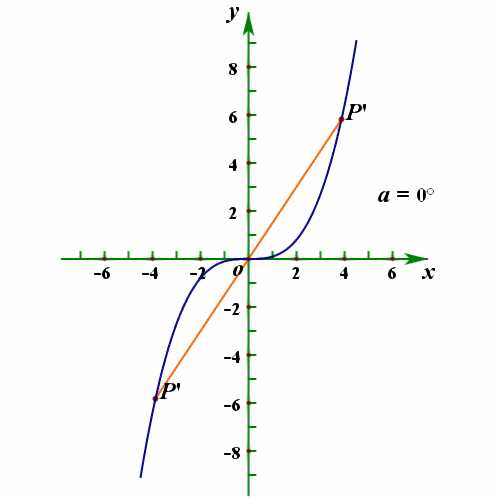
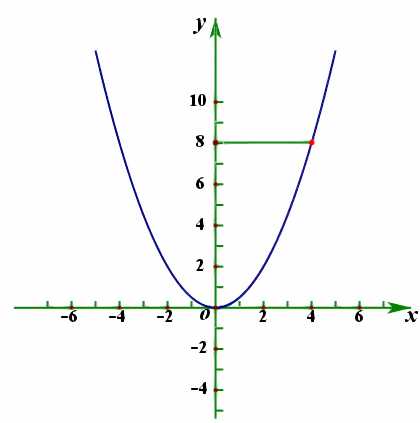
4、以图像的形式给出;
比如某函数图像关于原点对称,某函数图像关于\(y\)轴对称。
5、以奇偶性的性质应用的结论形式给出;
在公共定义域上,以下结论是成立的,也是可以证明的;
\(“奇+奇”\)是奇,
如\(f(x)=x+sinx\);\(g(x)=x^3+2sinx\);\(h(x)=x+\cfrac{1}{x}\);\(h(x)=2x+\cfrac{3}{x}\);
\(“奇-奇”\)是奇,
如\(f(x)=x^3-sinx\);\(h(x)=x-\cfrac{2}{x}\);
\(“奇\cdot奇”\)是偶,
如\(f(x)=x\cdot sinx\);\(f(x)=x^3sinx\);
\(“奇÷奇”\)是偶;
如\(f(x)=\cfrac{sinx}{x}\);
\(“偶+偶”\)是偶,\(“偶-偶”\)是偶;
\(“偶\cdot 偶”\)是偶,\(“偶÷偶”\)是偶;
\(“奇\cdot偶”\)是奇,\(“奇÷偶”\)是奇;
如\(f(x)\)为偶函数,则可知函数\(g(x)=xf(x)\)为奇函数。
如\(f(x)=e^x+\cfrac{1}{e^x}=e^x+e^{-x}\),偶函数;
如\(f(x)=e^x-\cfrac{1}{e^x}=e^x-e^{-x}\),奇函数;
6、以图像变换为依托给出,
如\(f(x-1)\)的对称轴是\(x=1\),则可知\(f(x)\)的对称轴是\(y\)轴,即\(f(x)\)是偶函数;
7、以周期性和对称性结合给出奇偶性;
已知函数\(f(x)\)的周期是2,且满足\(f(2+x)=f(-x)\),则可推知函数\(f(x)\)为偶函数。
具体变形如下:
由\(f(x+2)=f(x)\)和\(f(2+x)=f(-x)\),
得到\(f(-x)=f(x)\),
故函数\(f(x)\)为偶函数。
8、以结合赋值法给出;
已知函数\(f(x)\)满足\(f(1)=\cfrac{1}{2}\),且\(f(x+y)+f(x-y)=2f(x)f(y)\),则可推知函数\(f(x)\)为偶函数。
具体变形如下:
令\(x=y=0\),则有\(2f(0)=2f^2(0)\),得到\(f(0)=0\)或\(f(0)=1\);
再令\(x=1,y=0\),则有\(2f(1)=2f(1)f(0)\),得到\(f(0)=1\);
又题目已知\(f(1)=\cfrac{1}{2}\),得到\(f(0)=1\)[\(f(0)=0\)舍去];
再令\(x=0\),则得到\(f(y)+f(-y)=2f(0)f(y)=2f(y)\),
所以\(f(-y)=f(y)\),可知函数是偶函数。
9、以构造函数的形式给出或者得到奇偶性【难度大】;
具体例题请参见:例2
1、二次函数\(y=ax^2+bx+c(a\neq0)\) 为偶函数的充要条件是\(b=0\) ,
证明:对称轴为\(x=-\cfrac{b}{2a}\),
充分性:由\(b=0\),得到对称轴为\(x=0\),即就是\(y\)轴。
必要性:由函数为偶函数,对称轴是\(x=-\cfrac{b}{2a}\), 得到\(b=0\)。
由此推广得到以下结论:
2、多项式函数\(y=f(x)=ax^4+bx^3+cx^2+dx+e\) 为奇函数的充要条件是\(a=c=e=0\)
说明: \(f(-x)+f(x)=0\)恒成立,
即\([a(-x)^4+b(-x)^3+c(-x)^2+d(-x)+e]+(ax^4+bx^3+cx^2+dx+e)\)
\(=2ax^4+2cx^2+2e=0\),
即\(ax^4+cx^2+e=0\)对\(\forall x\in R\)都成立,故\(a=c=e=0\)。
比如,已知函数\(f(x)=x^3+(a-1)x^2+ax\)为奇函数,则\(a=1\);
3、多项式函数\(y=ax^4+bx^3+cx^2+dx+e\) 为偶函数的充要条件是\(b=d=0\)
仿上例可说明。
4、奇函数的导函数为偶函数;
文科:举例说明,比如函数\(f(x)=sinx\)为奇函数,其导函数为\(f'(x)=cosx\)为偶函数;
理科:逻辑证明,设函数\(f(x)\)为奇函数,其导函数\(f'(x)\),
记\(f'(x)=g(x)\),由函数\(f(x)\)为奇函数,
则有\(f(-x)+f(x)=0\),对其两边求导得到,
\(-f'(-x)+f'(x)=0\),即\(-g(-x)+g(x)=0\),
即\(g(-x)=g(x)\),
即函数\(g(x)\)为偶函数;
5、偶函数的导函数为奇函数;
文科:举例说明,比如函数\(f(x)=cosx\)为偶函数,其导函数为\(f'(x)=-sinx\)为奇函数;
理科:逻辑证明,设函数\(f(x)\)为偶函数,其导函数为\(f'(x)\),
记\(f'(x)=g(x)\),由函数\(f(x)\)为偶函数,
则有\(f(-x)-f(x)=0\),对其两边求导得到,
\(-f'(-x)-f'(x)=0\),即\(-g(-x)-g(x)=0\),
即\(g(-x)=-g(x)\),
即函数\(g(x)\)为奇函数;
6、若函数为奇函数,则在其关于原点对称的两点处的导函数的值相等。
文科:如\(f(x)=x^3\),则\(f'(x)=3x^2\),故\(f'(-1)=f'(1)=3\);
理科:如函数\(f(x)\)满足\(f(-x)+f(x)=0\),则给两边求导得到,
\(-f'(-x)+f'(x)=0\),则有\(f'(x_0)-f'(-x_0)=0\)
引申:对称性,若函数\(f(x)+f(2-x)=2\),则函数\(f(x)\)关于点\((1,1)\)对称,
且\(f'(x_0)=f'(2-x_0)\),比如\(f'(0)=f'(2)\);
7、若函数为偶函数,则在其关于原点对称的两点处的导函数的值互为相反数。
文科:如\(f(x)=x^2\),则\(f'(x)=2x\),故\(f'(-1)=-2,f'(1)=2\);
理科:如函数\(f(x)\)满足\(f(-x)-f(x)=0\),则给两边求导得到,
\(-f'(-x)-f'(x)=0\),则有\(f'(x_0)+f'(-x_0)=0\)
引申:对称性,若函数\(f(x)=f(2-x)\),则函数\(f(x)\)关于直线\(x=1\)对称,
且\(f'(x_0)=-f'(2-x_0)\),比如\(f'(0)=-f'(2)\);
标签:rac red sqrt alt 逻辑 .com gif https 构造
原文地址:https://www.cnblogs.com/wanghai0666/p/7674315.html