标签:jks des 情况 另一个 factor push git 分而治之 两种
Description
Makik 开了一家皮革制造厂,最近生意非常火。Makik 作为老板兼 CEO 兼客户经理,辛辛苦苦拉来了一位客户,他需要保证在接下来 \(N\) 个月间对这位客户持续供给皮革,第 \(i\) 个月需供应 \(A_i\) 张。由于养殖场的产量不稳定,皮革制造厂在不同月份间生产一张皮革的成本也不固定,第\(i\)个月生产每张皮革的成本为 \(C_i\).
Makik 可以提前制造好皮革并存放于 MS 仓库中,黑心的 MS 团队每个月需要对存放在仓库中的每张皮革收取 \(S\) 元的保管费用。假设 Makik 很有钱,MS 也很有钱,Makik 的工厂一个月可以生产任意多的皮革,MS 的仓库也可以存下任意多的皮革。请帮 Makik 算一算,为满足客户的要求,Makik 需要支出的总成本最低是多少?
Input
输入文件第一行包含两个整数 \(N\) 和 \(S\),分别表示需要供应皮革的月份数量和仓库保管费用。接下来 \(N\) 行,每行包含 \(2\) 个整数 \(C_i\) 和 \(A_i\),表示当月生产一张皮革的成本和皮革需求量。
Output
输出一行一个整数,需要支出的最低总成本。
明显\(DP\)啊, qwq
设\(f[i]\)代表前i个月中的最小单位价值(包括\(S\)
显然,某个月的皮革,要么是在之前某个月完成制作,要么是当前月完成.
且,会一次性完成.
所以转移很好想了.
\[
f[i]=min(f[i-1]+s,c)
\]
每次\(ans+=f[i]*a\)
不过貌似可以不开数组.emmm
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#define R register
using namespace std;
inline void in(long long &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
long long n,s,ans,c,a;
long long f[10008];
int main()
{
// freopen("factory.in","r",stdin);
// freopen("factory.out","w",stdout);
in(n),in(s);
for(R int i=1;i<=n;i++)f[i]=214748364766;
in(c),in(a);
f[1]=c;
ans+=f[1]*a;
for(R int i=2;i<=n;i++)
{
R long long c,a;
in(c),in(a);
f[i]=min(f[i-1]+s,c);
ans+=f[i]*a;
}
printf("%lld",ans);
fclose(stdin);
fclose(stdout);
return 0;
}Description
在 MS 国有\(N\) 座城市,编号从 \(1\) 到 \(N\) ,其中 \(1\) 号城市是 MS 国的首都。
MS 国里,只有一家铁路公司,经营着 \(M\) 条连接着各城市的铁路线路,每条线路都双向地连接着两座不同的城市。通过这些线路,我们可以在任意两座城市间通行。
原本,乘坐一条线路只需要花费 \(1\) 角钱。可是由于经营不善,铁路公司提出计划,要在今后的 \(Q\) 年间,每年给某一条线路涨价为 \(2\) 角钱。保证一条线路不会被涨价多次。
另外,这个铁路公司每年都会在每一座城市进行一次居民满意度调查。原本每一座城市中的居民都对铁路公司的服务十分满意,但在线路涨价后就说不定了。每一年的满意度调查都会在当年的涨价计划实施后进行。如果一座城市中的居民在当年坐火车去首都所需的最少花费相比于计划提出前增加了,他们就会对铁路公司抱有不满。首都的居民永远不会对铁路公司抱有不满。
在计划施行前,你需要帮助铁路公司统计出未来的每一年中,各将有多少城市的居民对铁路公司抱有不满。
Input
输入文件第一行包含三个正整数 \(N\), \(M\), \(Q\),分别表示 MS 国的城市数量、铁路路线数量和涨价计划将要实施的时间长度。
接下来 \(M\) 行,其中第 \(i\)行包含 \(2\) 个整数 \(U_i\) ,\(V_i\),表示第 \(i\) 条路线连接着编号为 \(U_i\) 和 \(V_i\) 的两座城市。
接下来 \(Q\) 行,其中第 \(j\) 行包含一个整数 \(R_j\),表示计划施行后第 \(j\) 年将会让第 \(R_j\) 条线路涨价。
Output
输出 \(Q\) 行,其中第 \(j\) 行表示第 \(j\) 年居民对铁路公司抱有不满的城市的数量。
不过貌似有人卡到了\(60pts\)?
最简单的一个做法就是跑从\(1\)开始跑\(Q\) 次\(Dijkstra\) 或者\(Spfa\)
每次与之前的最短路比较.
时间复杂度为\(O(Q\times mlogn)\)
下面的解释中会附带图片.
构图依据↓

首先需要明确的是,如果某一条铁路涨价,那么最短路经过它的城市都会不满.
PS:最短路不一定只有一种走法.例如根据样例构建出的图为这样.
\(\color{red} {边上的权为加入时的顺序}\)
\(5\)号节点到达\(1\)号节点就有两种走法.
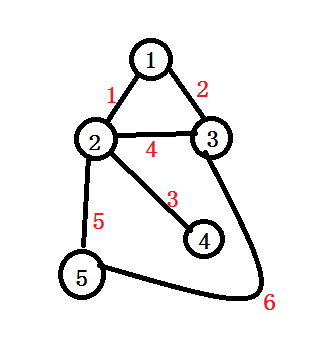
而给定我们的图中的边不一定都是合法的边(即跑最短路经过的边.
因此我们首先需要跑最短路,选出合法的边,从而建出一个合法的图。
但是考虑到我们的最短路可能会有一个中转点,来得到更小的价值.
所以建图的时候我们需要每次对一个被更新点的\(h\)数组重置.(\(h\)数组定义具体看代码。链式前向星.
其实接下来的两个图都是拓扑图!
对应最短路的图,我们构建出了一个只有合法的边的图.(如下
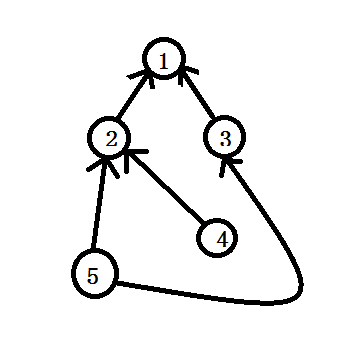
对于这个图,我们还需要构建出它的反图(应该也可以不建,不过处理起来会比较麻烦.
于是我们建造了反图.
上面的图就变成了这样↓
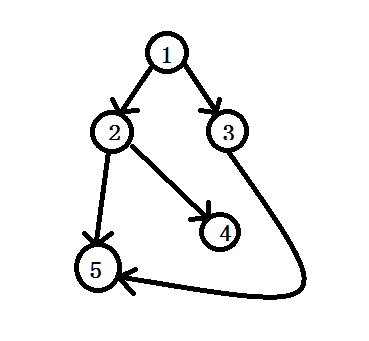
对应的我们删除一条新的边,我们可以将其所连的点的入度\(--\)
如果这个点的入度为0了,我们需要将与其相连的点的入度也\(--\),即这一路径被毁.
可以累加答案.
如果不理解的话还是动手画图试一试比较好,建图操作还是比较麻烦的.
建合法图是为了删边哦. qwq
#include<cstdio>
#include<queue>
#include<cstdlib>
#include<cstring>
#include<iostream>
#define R register
#define N 200008
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,m,q,to[N];
int head[N],h[N],dis[N],ins[N];
int tot=1,ttt=1;//这样是为了两两为一组,下面是/2 qwq
struct cod
{
int u,v,w,idx;
}edge[N<<1],e[N<<1];
bool vis[N],exist[N];
inline void add(int x,int y,int z,int idx)
{
edge[++tot].u=head[x];
edge[tot].v=y;
edge[tot].w=z;
edge[tot].idx=idx;
head[x]=tot;
}
inline void ado(int x,int y,int z,int idx)
{
e[++ttt].u=h[x];
e[ttt].v=y;
e[ttt].w=z;
e[ttt].idx=idx;
h[x]=ttt;
}
inline void spfa()
{
for(R int i=2;i<=n;i++)
dis[i]=214748364,vis[i]=false;
queue<int>q;dis[1]=0;
q.push(1);
while(!q.empty())
{
int u=q.front();q.pop();vis[u]=false;
for(R int i=head[u];i;i=edge[i].u)
{
if(dis[edge[i].v]>dis[u]+edge[i].w)
{
dis[edge[i].v]=dis[u]+edge[i].w;
h[edge[i].v]=0;//注意这里要清零.
ado(edge[i].v,u,edge[i].w,i/2);
if(vis[edge[i].v]==false)
{
vis[edge[i].v]=true;
q.push(edge[i].v);
}
}
else if(dis[edge[i].v]== dis[u]+edge[i].w)
{
ado(edge[i].v,u,edge[i].w,i/2);
}
}
}
}
int main()
{
// freopen("trainfair.in","r",stdin);
// freopen("trainfair.out","w",stdout);
in(n),in(m),in(q);
for(R int i=1,x,y;i<=m;i++)
{
in(x),in(y);
add(x,y,1,i);add(y,x,1,i);
exist[i]=true;
}
spfa();
for(R int i=1;i<=n;i++)head[i]=0;tot=1;
for(R int i=1;i<=n;i++)
{
for(R int j=h[i];j;j=e[j].u)
{
ins[i]++;to[e[j].idx]=i;
add(e[j].v,i,e[j].w,e[j].idx);
}
}
for(R int x,ans=0;q;q--)
{
in(x);
if(!exist[x] or to[x]==0)
{
printf("%d\n",ans);
continue;
}
ins[to[x]]--;
exist[x]=false;
if(ins[to[x]]==0)
{
queue<int>Q;
Q.push(to[x]);
while(!Q.empty())
{
int u=Q.front();Q.pop();ans++;
for(R int i=head[u];i;i=edge[i].u)
{
if(!exist[edge[i].idx])continue;
exist[edge[i].idx]=false;
ins[edge[i].v]--;
if(!ins[edge[i].v])
Q.push(edge[i].v);
}
}
}
printf("%d\n",ans);
}
fclose(stdin);
fclose(stdout);
return 0;
}Description
给定一个长度为 \(n\)的序列 \(a\),请你算一算这个式子:
\[ \sum\limits_{i=1}^n\sum\limits_{j=i}^n(j-i+1)\min(a_i,a_{i+1},\dots,a_{j})\max(a_i,a_{i+1},\dots,a_{j}) \]
由于高精度写起来太麻烦了,请将答案对 \(10^9\) 取模后输出。
Input
输入文件第一行包含两个数字 \(n\), 表示序列 \(a\) 的长度。
接下来一行包含 \(n\) 个数字,依次表示序列中的元素 \(a_1,a_2,...,a_n\)。
Output
输出式子的值对\(10^9\)取模后的结果。
"woc,这么简单的模拟题 ! " 直接\(for\)循环模拟的话,只会得到20pts
首先明确一句话
\(\color{red}{求一段区间内所有子区间和的东西,考虑}\) \(\color{gold}{分治}\)
什么?
\(\color{red}{分治即为分而治之}.\)
内容来自百度百科.
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分目标完成程序算法,简单问题可用二分法完成。
如果用来解题呢?
我们发现,对于某一个最大值和最小值,在区间上的分布会存在如下三种情况.
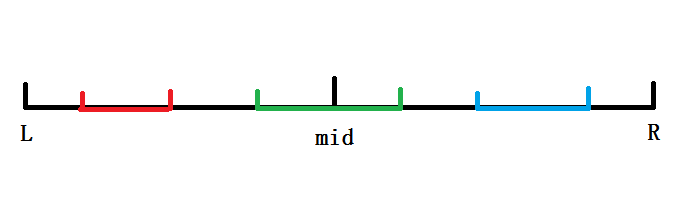
而难点在于如何计算跨过\(mid\)的部分对答案的贡献.
枚举一个端点.去计算另一个端点的贡献。
(下面的解释与代码部分并不符合)
对于此题,我们从\(l->mid\)枚举左端点\(x\),令\([x,mid]\)的最小值为\(a\),最大值为\(b\).
我们分别维护两个指针\(i,j\)从\(mid+1\)向右走. 右端点为\(r\)
\(i\)指针维护右侧到哪个位置满足\(a_{mid+1}\dots a_r\) \(\geq a\)
\(j\)指针维护右侧到哪个位置满足\(a_{mid+1}\dots a_r \leq b\)
对于右端点\(y\),存在如下三种情况.(这里按照 \(i<j\)讨论)
\[ ans+=a\times b \times \sum_{y=mid+1} ^{a}(y-x+1) \]
这个时候,由于区间长度满足等差数列,所以根据等差数列去求解即可.
等差数列的求和公式
\[
S_n=na_1+\frac{n(n-1)}{2}d,n\in N^{*}
\]
此时最小值\(a\)不可用.我们需要将式子变形,先将最大值\(b\)提出来.
\[
ans+=b \times \sum_{y=i+1}^{j}min*(y-x+1)
\\=b \times (\sum_{y=i+1}^{j}min \times y - \sum_{y=i+1}^{j}min \times (x-1))
\]
具体min的意义,就是\([i+1,j]\)中的最小值.
此时预处理出来\(\sum_{y=i+1}^{b} min \times j\) 和\(\sum_{y=i+1}^{b}min\)即可
此时最小值\(a\)和最大值\(b\)都不可用.
我们继续把式子变形.
\[
ans+=\sum_{y=j+1}^{r}min \times max \times (y-x+1)
\\=\sum_{y=j+1}^{r}max\times min \times y-\sum_{y=j+1}^{r}max\times min \times (x-1)
\]
此时,预处理出\(\sum_{y=j+1}^{r}max\times min \times y\)与\(\sum_{y=j+1}^{r}max\times min\)即可.
这题恶心死了
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<cctype>
#define int long long
#define mod 1000000000
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,a[500005],ans;
int sumx[500005],sumn[500005],csumx[500005],csumn[500005],mxmn[500005];
int cmxmn[500005];
inline void CDQ(int l,int r)
{
if(l==r)
{
(ans+=a[l]*a[l])%=mod;
return ;
}
int mid=(l+r)>>1;
CDQ(l,mid),CDQ(mid+1,r);
int mx=0,mn=214748364766;
sumx[mid]=sumn[mid]=csumx[mid]=csumn[mid]=mxmn[mid]=cmxmn[mid]=0;
for(R int i=mid+1;i<=r;i++)
{
mx=max(mx,a[i]),mn=min(mn,a[i]);
sumx[i]=(sumx[i-1]+mx)%mod;
sumn[i]=(sumn[i-1]+mn)%mod;
csumx[i]=(csumx[i-1]+mx*i%mod)%mod;
csumn[i]=(csumn[i-1]+mn*i%mod)%mod;
mxmn[i]=(mxmn[i-1]+mx*mn%mod)%mod;
cmxmn[i]=(cmxmn[i-1]+mx*mn%mod*i%mod)%mod;
}
R int j=mid,k=mid;
mx=0,mn=214748364766;
for(R int i=mid;i>=l;i--)
{
mx=max(mx,a[i]);mn=min(mn,a[i]);
while(j<r and a[j]>=mn and a[j+1]>=mn)j++;
while(k<r and a[k]<=mx and a[k+1]<=mx)k++;
R int a=min(j,k),b=max(j,k);
(ans+=mx*mn%mod*((a-i+1+mid-i+1+1)*(a-mid)/2%mod))%=mod;
(ans+=cmxmn[r]-cmxmn[b]-(i-1)*(mxmn[r]-mxmn[b])%mod+mod)%=mod;
if(j<k) (ans+=mx*(csumn[b]-csumn[a]-(i-1)*(sumn[b]-sumn[a])%mod))%=mod;
else (ans+=mn*(csumx[b]-csumx[a]-(i-1)*(sumx[b]-sumx[a])%mod)%mod)%=mod;
(ans+=mod)%=mod;
}
}
signed main()
{
// freopen("math.in","r",stdin);
// freopen("math.out","w",stdout);
in(n);
for(R int i=1;i<=n;i++)in(a[i]);
CDQ(1,n);
printf("%lld",(ans+mod)%mod);
fclose(stdin);
fclose(stdout);
return 0;
}标签:jks des 情况 另一个 factor push git 分而治之 两种
原文地址:https://www.cnblogs.com/-guz/p/9745259.html