标签:连接 固定 必须 continue 分享 return cdn 修改 说明
物流公司要把一批货物从码头A运到码头B。由于货物量比较大,需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线,以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在,有的时候某个码头会无法装卸货物。这时候就必须修改运输路线,让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情,会带来额外的成本。因此物流公司希望能够订一个n天的运输计划,使得总成本尽可能地小。
输入格式:
第一行是四个整数\(n(l≤n≤100)、m(l≤m≤20)、K\)和\(e\)。\(n\)表示货物运输所需天数,\(m\)表示码头总数,\(K\)表示每次修改运输路线所需成本,\(e\)表示航线条数。接下来\(e\)行每行是一条航线描述,包括了三个整数,依次表示航线连接的两个码头编号以及航线长度\((>0)\)。其中码头\(A\)编号为\(1\),码头\(B\)编号为\(m\)。单位长度的运输费用为\(1\)。航线是双向的。再接下来一行是一个整数\(d\),后面的\(d\)行每行是三个整数\(P(1<P<m),a,b(1≤a≤b≤n)\)。表示编号为\(P\)的码头从第\(a\)天到第\(b\)天无法装卸货物(含头尾)。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头\(A\)到码头\(B\)的运输路线。
输出格式:
包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。
输入样例#1: 复制
5 5 10 8
1 2 1
1 3 3
1 4 2
2 3 2
2 4 4
3 4 1
3 5 2
4 5 2
4
2 2 3
3 1 1
3 3 3
4 4 5
输出样例#1: 复制
32
【样例输入说明】
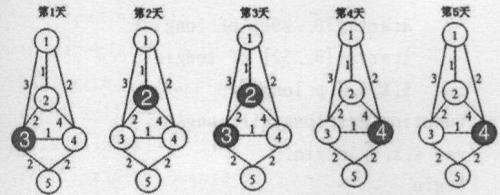
上图依次表示第1至第5天的情况,阴影表示不可用的码头。
【样例输出说明】
前三天走1-4-5,后两天走1-3-5,这样总成本为(2+2)3+(3+2)2+10=32。
一道非常好的题目。因为我太菜了做不出
这道题目很明显的可以看出是个dp
因为我们的目的是话费最小,就是考虑换不换路线这个操作。
因为\(m\)值奇小。所以我们可以一边dp一边跑最短路。
最短路这个应该不说都知道吧。
这样我们枚举每天的情况。
\(dp[i]\)表示第i天的最小消费。
那么整个题目我们要考虑的就是一条最短路在合法时用多久了。
因为影响答案最优的就是每次换路的花费。
那么我们就枚举第\(i\)到\(j\)天用当前合法的最短路就可以了。
方程就是
\(dp[i]=min(dp[i],dp[j-1]+最短路*(i-j+1)+k)\)
floyd版
当时打炸了。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;
const int N=21;
int n,m,k,l,q,vis[N];
int u[N*10],v[N*10],z[N*10];
int ch[N][101],f[101],dis[N][N];
int read(){
int x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*w;
}
void floyd(){
memset(dis,63,sizeof(dis));
for(int i=1;i<=l;i++)
dis[u[i]][v[i]]=dis[v[i]][u[i]]=z[i];
for(int p=1;p<=m;p++)
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++){
if(i!=j&&j!=p&&p!=i&&!vis[i]&&!vis[j]&&!vis[p]){
if(dis[i][j]>dis[p][j]+dis[i][p])
dis[i][j]=dis[i][p]+dis[p][j];
}
}
}
int main(){
n=read();m=read();k=read();l=read();
for(int i=1;i<=l;i++){
u[i]=read(),v[i]=read(),z[i]=read();
}
q=read();
for(int i=1;i<=q;i++){
int x=read(),lx=read(),rx=read();
for(int j=lx;j<=rx;j++)
ch[x][j]=1;
}
memset(f,63,sizeof(f));f[0]=-k;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)vis[j]=0;
for(int j=i;j>=1;j--){
for(int p=1;p<=m;p++)
vis[p]|=ch[p][j];
floyd();if(dis[1][m]==dis[0][0])continue;
f[i]=min(f[i],f[j-1]+(i-j+1)*dis[1][m]+k);
}
}
printf("%d\n",f[n]);
return 0;
}spfa版
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<iostream>
using namespace std;
const int N=21;
int n,m,k,l,q,vis[N],inf;
int u[N*10],v[N*10],z[N*10];
int ch[N][101],f[101],dis[N][N];
int read(){
int x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*w;
}
int spfa(){
queue<int>q;q.push(1);
int dist[21],ff[21];
memset(dist,63,sizeof(dist));inf=dist[0];
memset(ff,0,sizeof(ff));dist[1]=0;ff[1]=1;
while(!q.empty()){
int u=q.front();q.pop();
ff[u]=0;
for(int i=1;i<=m;i++){
if(vis[i])continue;
if(dis[u][i]&&dist[i]>dist[u]+dis[u][i]){
dist[i]=dist[u]+dis[u][i];
if(!ff[i]){
q.push(i);ff[i]=1;
}
}
}
}return dist[m];
}
int main(){
n=read();m=read();k=read();l=read();
for(int i=1;i<=l;i++){
//u[i]=read(),v[i]=read(),z[i]=read();
int x=read(),y=read(),vi=read();
dis[x][y]=dis[y][x]=vi;
}
q=read();
for(int i=1;i<=q;i++){
int x=read(),lx=read(),rx=read();
for(int j=lx;j<=rx;j++)
ch[x][j]=1;
}
memset(f,63,sizeof(f));f[0]=-k;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)vis[j]=0;
for(int j=i;j>=1;j--){
for(int p=1;p<=m;p++)
vis[p]|=ch[p][j];
int vi=spfa();
if(vi==inf)continue;
f[i]=min(f[i],f[j-1]+(i-j+1)*vi+k);
}
}
printf("%d\n",f[n]);
return 0;
}dijkstra就咕掉了。
[luogu] P1772 [ZJOI2006]物流运输(动态规划,最短路)
标签:连接 固定 必须 continue 分享 return cdn 修改 说明
原文地址:https://www.cnblogs.com/hhh1109/p/9745780.html