标签：png 分享图片 sqrt line 部分 解决 递增 lan 阶段
1 图象法：如果\(f(x)\)是以图象形式给出的，或者\(f(x)\)的图象易作出，可由图象的直观性写出它的单调性区间．
\(\fbox{例1}\)【2018天津模拟改编】
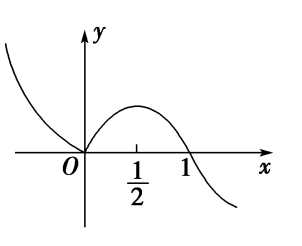
已知函数\(y=f(x)(x\in R)\)的图像如图所示，则函数\(f(x)\)的单调区间为_____________。
分析：由图可知，函数\(f(x)\)在区间\((-\infty，0)\)和\([\cfrac{1}{2}，+\infty)\)上单调递减，
在区间\([0，\cfrac{1}{2}]\)上单调递增，
【点评】：①学会读图，解读图像时，是将变化趋势一致(仅仅上升或仅仅下降)的那部分图像，向\(x\)轴做射影，所得的区间即为单调区间。
②这一方法可以解决高中阶段的许多简单函数的单调性，比如基本初等函数，一次、二次函数等，
2 定义法：先求定义域，再利用单调性定义．
\(\fbox{例2}\)【题目自拟，这一方法很少用】
利用定义法求函数\(f(x)=x-\cfrac{1}{x}\)的单调区间。
分析：定义域为\((-\infty，0)\cup(0，+\infty)\)；
任取\(x_1<x_2\in (0，+\infty)\)，
则\(f(x_1)-f(x_2)=x_1-\cfrac{1}{x_1}-(x_2-\cfrac{1}{x_2})\)
\(=(x_1-x_2)-(\cfrac{1}{x_1}-\cfrac{1}{x_2})\)
\(=(x_1-x_2)-\cfrac{x_2-x_1}{x_1x_2}\)
\(=(x_1-x_2)+\cfrac{x_1-x_2}{x_1x_2}\)
\(=(x_1-x_2)(1+\cfrac{1}{x_1x_2})<0\)
即\(f(x_1)<f(x_2)\)，
故函数\(f(x)=x-\cfrac{1}{x}\)在区间\((0，+\infty)\)上单调递增；
同理可以证明函数\(f(x)=x-\cfrac{1}{x}\)在区间\((-\infty，0)\)上单调递增；
[或者利用\(f(x)\)为奇函数，可以证明在区间\((-\infty，0)\)上单调递增]
【点评】：①以上述题目为例，如果在区间\((0，+\infty)\)上\(f(x_1)-f(x_2)\)的差值不能确定一定为正或为负，
则说明需要再寻找新的分点，将上述的区间细化，比如将上述区间\((0，+\infty)\)细化为\((0，x_0)\)和\((x_0，+\infty)\)，
然后分别在区间\((0，x_0)\)和区间\((x_0，+\infty)\)上判断\(f(x_1)-f(x_2)\)的正负，从而确定单调区间。
②注意有效使用函数的奇偶性，简化证明。
3 利用已知函数的单调性，即转化为已知函数的和、差或复合函数，求单调区间。
\(\fbox{例3}\)【待编辑】
4 导数法：利用导数取值的正负确定函数的单调区间。【高中阶段使用的主要方法，通法】
详见博文：导数法判断函数的单调性的策略
(1)确定函数的定义域．
(2)将复合函数分解成基本初等函数\(y＝f(u)\)，\(u＝g(x)\)．
(3)分别确定这两个函数的单调区间．
(4)若这两个函数同增同减，则\(y＝f(g(x))\)为增函数；若一增一减，则\(y＝f(g(x))\)为减函数，即“同增异减”。
\(\fbox{例5}\)【求复合函数的单调性】
已知函数\(f(x)=log_2(x^2-3x+2)\)，求其单调区间。
分析：令\(u=x^2-3x+2\)，
则原复合函数拆分为外函数\(y=f(u)=log_2u\)和内函数\(u=x^2-3x+2\)
由\(u=x^2-3x+2>0\)，解得\(x\in (-\infty，1)\cup(2，+\infty)\)，
即此复合函数的定义域为\(x\in (-\infty，1)\cup(2，+\infty)\)。
那么要研究其单调性，必须先在上述定义域范围内，定义域优先原则。
然后由\(u=x^2-3x+2=(x-\cfrac{3}{2})^2-\cfrac{1}{4}\)，
则内函数\(u(x)\)在区间\((-\infty，1)\)上单调递减，在区间\((2，+\infty)\)上单调递增，
而外函数\(y=f(u)=log_2u\)在\((0，+\infty)\)上单调递增，
故复合函数\(f(x)\)在区间\((-\infty，1)\)上单调递减，在区间\((2，+\infty)\)上单调递增。
\(\fbox{例6}\)【求复合函数的单调区间】【2018天津模拟】
已知函数\(y=f(x)(x\in R)\)的图像如图所示，则函数\(g(x)=f(log_ax)(0<a<1)\)的单调递减区间为【】
\(A、[0，\cfrac{1}{2}]\) \(\hspace{4em}\) \(B、[\sqrt{a}，1]\)
\(C、(-\infty，0)\cup[\cfrac{1}{2}，+\infty)\) \(\hspace{4em}\) \(D、[\sqrt{a}，\sqrt{a+1}]\)
分析：由图可知，外函数\(f(x)\)在区间\((-\infty，0)\)和\([\cfrac{1}{2}，+\infty)\)上单调递减，
在区间\([0，\cfrac{1}{2}]\)上单调递增，
又\(0<a<1\)时，内函数\(y=log_ax\)在区间\((0，+\infty)\)上单调递减，
故要使得复合函数函数\(g(x)=f(log_ax)(0<a<1)\)单调递减，
则需要\(log_ax\in [0，\cfrac{1}{2}]\)，即\(0\leq log_ax\leq \cfrac{1}{2}\)，
解得\(x\in [\sqrt{a}，1]\)，故选B。
标签：png 分享图片 sqrt line 部分 解决 递增 lan 阶段
原文地址：https://www.cnblogs.com/wanghai0666/p/9744987.html
