标签：img   print   http   fabs   code   ons   ble   高效   turn   

概述

牛顿迭代法是一种数值算法，可以用于求函数的零点。其思想在于把函数抽象为直线，一步步用估计逼近函数的零点。

其逼近速度非常有效，常常在十几步迭代内就能求得非常精确的结果，十分高效。

引理

考虑在如下坐标系\(xOy\)中的一条直线：

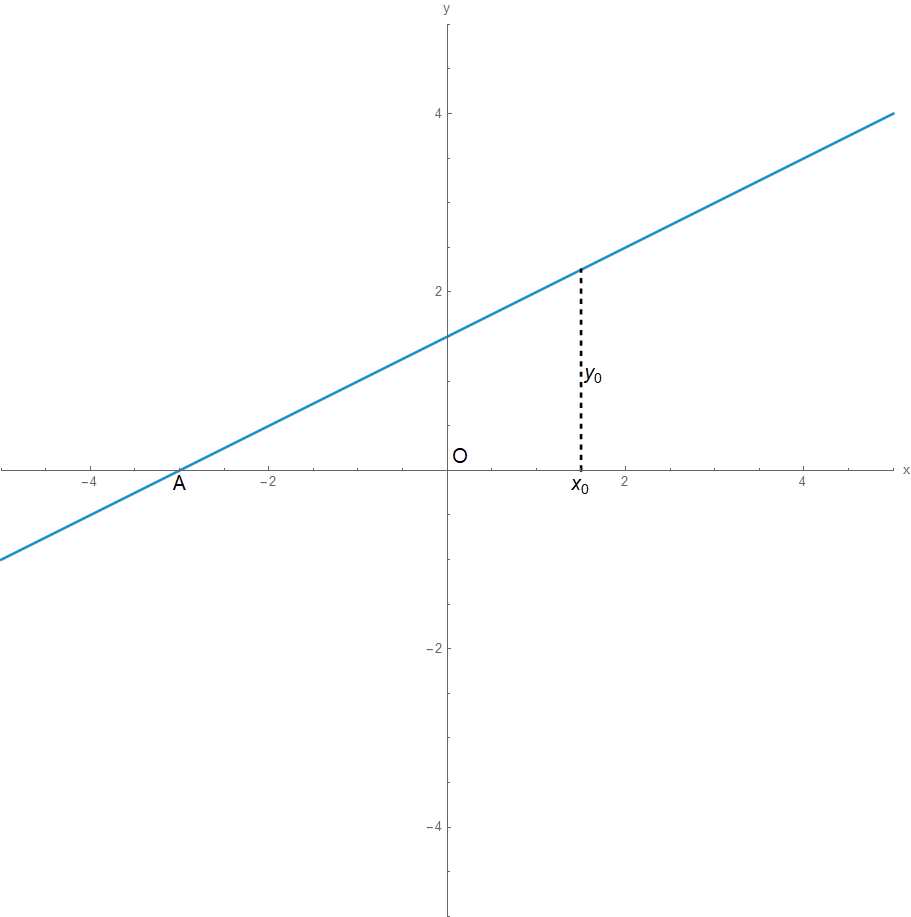
其值在\(x=x_0\)时取值为\(y_0\)。那么这条直线与\(x\)轴的交点的\(x\)坐标\(A\)为多少？

设这条直线的解析式为\(y=kx+b\)，则有
\[ y_0=kx_0+b \]

即
\[ b=y_0-kx_0 \]

令\(y=0\)，得方程
\[ kx+y_0-kx_0=0 \]

解得
\[ x=\frac{kx_0-y_0}{k} \]

即

\[ x=x_0-\frac{y_0}{k} \]

牛顿迭代法

我们正式开始使用牛顿迭代法求函数\(f(x)\)的零点。

问题：试求\(\sqrt{2}\)的近似值。

原命题等价于求函数\(f(x)=x^2-2\)的零点。

第一步：猜测初始值

首先我们随便猜测一个值。不妨设为\(x=4\)吧。

第二步：迭代

过\((x,f(x))\)点作\(f(x)\)的切线，得到：

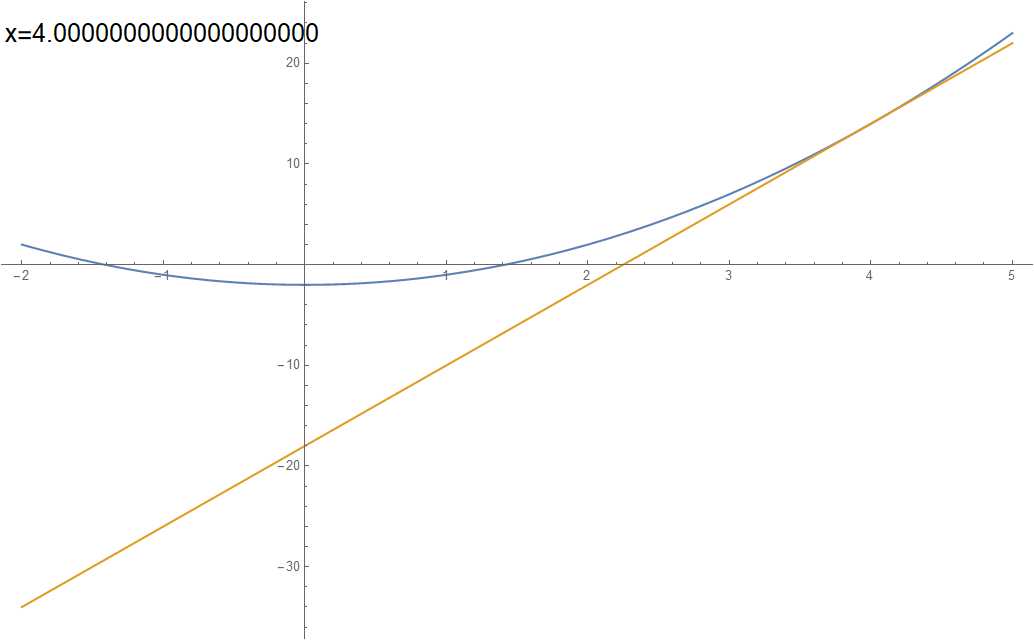
根据导数的几何意义，这条直线的斜率为\(f'(x)\)，则根据我们前面得到的结论，这个函数与\(x\)轴的交点的\(x\)坐标为
\[ x'=x-\frac{f(x)}{f'(x)} \]

根据最理想的估计，如果导数不变的话，零点应该就在那个位置。那么我们令\(x=x'\)，这称为一次迭代。

回到例子。\(f(x)=x^2-2\)，则\(f'(x)=2x\)，则有：
\[ x'=x-\frac{f(x)}{f'(x)}=x-\frac{x^2-2}{2x}=\frac{x}{2}+\frac{1}{x} \]

每次用\(\frac{x}{2}+\frac{1}{x}\)替代\(x\)，重复以上过程：

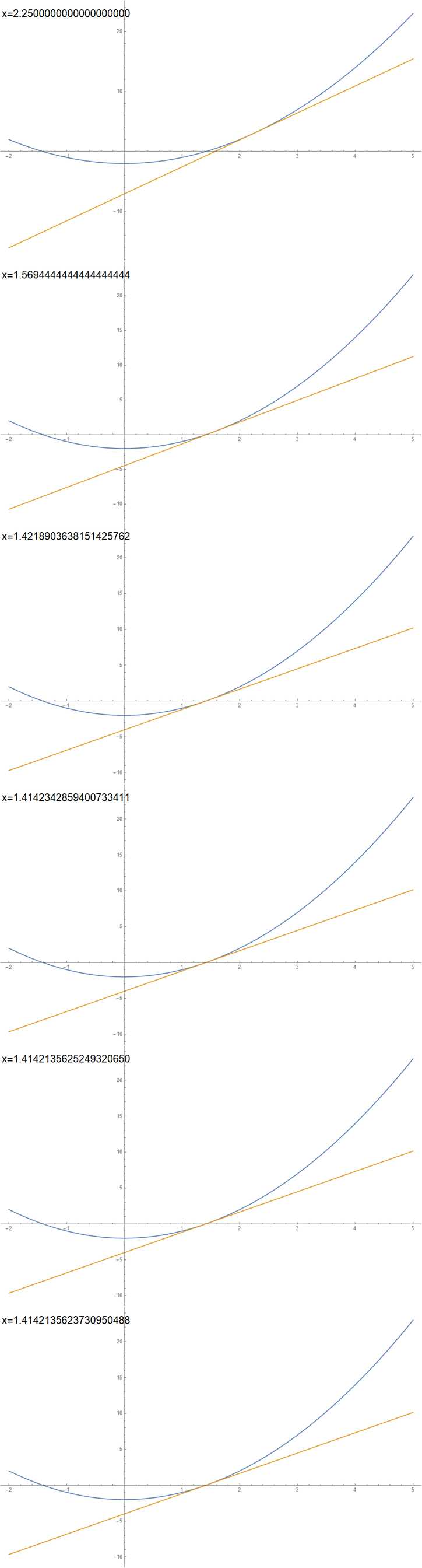
可以看到，仅仅进行了六次迭代，就得到了\(20\)位的精确值。

程序如下：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const double eps=1e-10;
double a,x;
double f(double x){return x*x-a;}
double df(double x){return 2*x;}
int main(){
    scanf("%lf",&a);
    x=1;
    while(fabs(f(x))>=eps)x-=f(x)/df(x);
    printf("%.10lf\n",x);
} 

直观理解牛顿迭代法

标签：img   print   http   fabs   code   ons   ble   高效   turn   

原文地址：https://www.cnblogs.com/eztjy/p/9747440.html