标签:穷举法 break end div 时间复杂度 image pac namespace names
一:三种基本的素数判定
1:穷举法:适用于数据较小的时候。时间复杂度:O(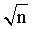 )
)
int isPrime(int n) { if(n==1||n==0) return 0; int m = sqrt(n+0.5); for(int i = 2; i <= m; i++) if(n%i==0) return 0; return 1; }
2:埃拉托瑟尼筛法求素数 时间复杂度:O(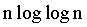 )
)
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int maxn = 1e6; int book[maxn]; int prime[maxn]; int main(void) { int n; int num; while(~scanf("%d",&n)) { num = 0; for(int i = 2; i <= n; i++) { if(book[i]==0) prime[num++] = i; for(int j = i * i; j <= n; j += i) { book[j] = 1; } } for(int i = 0; i < num; i++) cout<<prime[i]<<endl; } return 0; }
3:欧拉筛法
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int maxn = 1e6; int prime[maxn]; int book[maxn]; int main(void) { int n; int num; while (~scanf("%d", &n)) { num = 0; for (int i = 2; i <= n; i++) { if (book[i]==0) prime[num++] = i; for (int j = 0; j < num; j++) { if (i*prime[j] > n) break; // 过大的时候跳出 book[i*prime[j]] = 1; if ((i%prime[j]) == 0) // 如果i是一个合数,而且i % prime[j] == 0 break; } } for (int i = 0; i < num; i++) printf("%d\n", prime[i]); } return 0; }
标签:穷举法 break end div 时间复杂度 image pac namespace names
原文地址:https://www.cnblogs.com/AC-AC/p/9749889.html