唯一分解定理

标签：span   class   bing   特殊情况   .com   ==   info   http   技术分享   

唯一分解定理内容：每个正整数都可以分解成若干质数的乘积，质数从小到大排列（乘积可以是0,1,2......）

用数学式子表示则：对任一整数a＞1，有a= (p1^a1)*(p2^a2)…(pn^an) ，其中p1<p2<…<pn均为素数，而a1,a2…,an是正整数。（1是个特殊情况，不算入）

那么，背记重点来了：

1.a的正约数的个数：（每个都是从a0到an）

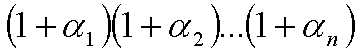
举个例子：

　　a=40=2^3*5^1；

　　n=(1+3)(1+1)=8;

　　1 40 2 20 4 10 5 8

2.a的正约数的和为：

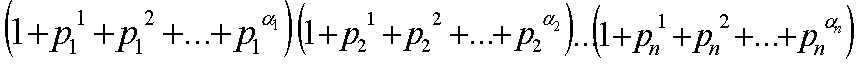
　　还是上面的例子

　　sum=90；

　　sum=（1+2+4+8）（1+5）=90，bingo！

3.a的欧拉函数

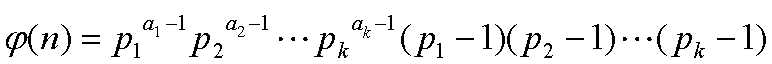
 　　fy（40）=16；

　　fy（40）=2^2*5^0*(2-1)*(5-1)=16,bingo!

应用：

1.求n的质因数分解：

 1 k=2;
 2 while (k*k<=a)
 3     {if (a%k==0) 
 4         while (a%k==0)
 5             {
 6              a/=k; …//对因子重数的其他处理 
 7              }
 8      k++;
 9     }
10 if (a>1) …//再对分解最后的那个质数进行处理 

2.求n的约数和

 1 int sum ( int n )
 2 {int k, res, tmp;
 3  k=2; res=1;
 4  while (k*k<=a)
 5     {tmp=1;
 6       while (n%k==0) {n/=k;tmp=tmp*k+1;} 
 7       res*=tmp;
 8       k++;
 9     }
10  if (n>1)  res*=(1+n);
11  return res;
12 } 

唯一分解定理

标签：span   class   bing   特殊情况   .com   ==   info   http   技术分享   

原文地址：https://www.cnblogs.com/SUMMER20020929/p/9751764.html