标签:bubuko 有一个 image 线性筛 结果 组合数 space nbsp 不同的
这三个题思路都不复杂,就放在一起
计算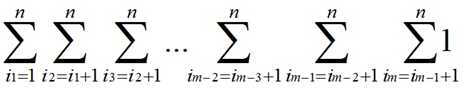
由于最终结果可能超过int的范围,因此请将运算结果对1000000007取模。
一个整数T(T <= 200000),表示数据组数。每行两个整数m, n。(0 < m <= n <= 2000)
就是求组合数啊 C(n,m)
想一想一层套一层的循环,每一次都要从前一个数+1开始,不是等价于前一个循环中,有一个数被选择了,还剩下的数从+1开始,相当于在这一层循环里去挑一个出来啊。
#include<bits/stdc++.h> using namespace std; #define N 2020 #define ll long long #define mod 1000000007 ll t,n,m; ll c[N][N]; int main() { c[1][0]=c[1][1]=1; for(ll i=2;i<=2011;i++) { c[i][0]=1; for(ll j=1;j<=2011;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; } scanf("%lld",&t); while(t--) { scanf("%lld%lld",&m,&n); printf("%lld\n",c[n][m]); } return 0; }
N个同学参加比赛,问有多少种排名情况,允许出现并列的情况(N<=12)
这个题老师放了水,原题N<=200,但是思路是一样的
考虑谁当第一,比如对于n=4是,可以在四个中选一个当第一,也可以选两个,选三个,选四个
所以有ans[4]=c(4,1)*ans[3]+c(4,2)*ans[2]+c(4,3)*ans[1]+c(4,4)*ans[0]
所以n可以类似的去算,可以得到这样的一个计算方式
#include<bits/stdc++.h> using namespace std; #define N 20 #define ll long long ll n,a[N],c[N][N]; ll dfs(ll x) { if(x==0)return 1; if(a[x])return a[x]; for(int i=1;i<=x;i++) a[x]+=c[x][i]*dfs(x-i); return a[x]; } int main() { cin>>n; c[1][1]=c[1][0]=1; for(ll i=2;i<=14;i++) { c[i][0]=1; for(ll j=1;j<=14;j++) c[i][j]=c[i-1][j]+c[i-1][j-1]; } cout<<dfs(n); }
OtosakaYuu最近为了Nao Tomori拯救世界而立了一个flag,于是他想了一道数学题。有一个正整数数列a1,a2…an。定义函数f(x)为x的不同的质因数数量。求f(a1),f(a2)…f(an)。
第一行包含一个正整数,表示n。接下来n行,每行包含一个正整数ai。1<=n<=1000000,2<=ai<=1000000
只能o(1)地做,在线性筛上加特判
对于一个被prime[j]筛出来的数,考虑和prime[j]相乘的i是否能整除prime[j],如果可以,证明i*prime[j]已经有prime[j]这个因数了,如果不可以,那它的质因数数目会在i的质因数数目的基础上+1
#include<bits/stdc++.h> using namespace std; #define N 1000100 #define mx 1000010 #define ll long long ll t,n,cnt,c,k,mm; ll s[N],f[N],v[N],num[N],prime[N]; void primes(int n) { num[1]=1; for(int i=2;i<=n;i++) { if(!v[i]) { prime[++cnt]=i; v[i]=i;num[i]=1; } for(int j=1;j<=cnt;j++) { if(prime[j]>v[i]||prime[j]>n/i)break; v[i*prime[j]]=prime[j]; if(i%prime[j])num[i*prime[j]]=num[i]+1; else num[i*prime[j]]=num[i]; } } } int main() { scanf("%lld",&t); primes(mx); for(int i=1;i<=t;i++) { scanf("%lld",&k); printf("%lld\n",num[k]); } }
标签:bubuko 有一个 image 线性筛 结果 组合数 space nbsp 不同的
原文地址:https://www.cnblogs.com/NSD-email0820/p/9757119.html