Longest Common Substring($LCS$)

标签：介绍   两种   因此   sub   str   end   gis   定义   math   

Longest Common Substring(\(LCS\))

什么是子序列?

　　子序列就是某一个序列的不连续的一部分.

如图， \(abcde\)就是图中序列的一个子序列。

公共子序列

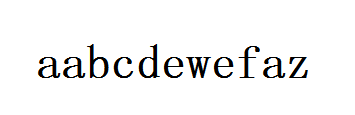
　　公共子序列的定义就是两个序列共有的子序列啦. qwq

一些题目就会要求我们求两个序列的最长公共子序列。

如果直接去两两比对的话,复杂度爆炸!

所以介绍\(O(n\times m)\)做法.

\(Dp\)

我们设\(f[i][j]\)代表从到达\(a\)串第\(i\)个位置,\(b\)串第\(j\)个位置的最长公共子序列的长度.

如何状态转移？

我们发现,如果要使我们的公共子序列的长度加长,必须要有的条件为\(a[i]==b[j]\)

因此,存在两种情况.

一. \(a[i]==a[j]\)

状态转移方程
\[ f[i][j]=f[i-1][j-1]+1 \]
这时直接继承上一个情况即可.

二.\(a[i]!=a[j]\)

此时需要考虑的是,我们依旧要进行状态的传递.

当前\(f[i][j]\)需要继承上一状态取到\(max\)。

那这里的上一状态是什么?

　我们可以知道的是,\(i-1\)位置与\(j\)位置已经有解,\(i\)位置与\(j-1\)位置已经有解。

如何去做?当前位置继承可以选择的状态也就是上面两种状态.

因此状态转移方程为
\[ f[i][j]=max(f[i-1][j],f[i][j-1]) \]
这样为什么正确?

我们当前位置为\(a\)串\(i\)和\(b\)串\(j\),最长公共子序列可能是\(a\)串\(i-1\)位置与\(b\)串\(j\)位置结合,

状态转移方程

\[\begin{cases}f[i][j]=f[i-1][j-1]+1　(a[i]==a[j]) \\f[i][j]=max(f[i-1][j],f[i][j-1])　(a[i]!=a[j])\\\end{cases}\]

由于当前位置\(i\)的状态只会与上一位置\(i-1\)有关,因此我们可以滚动数组.

滚动数组就不多BB了 emmm,

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#define R register
using namespace std;
char a[5008],b[5008];
int lena,lenb;
int f[2][5008];
int main()
{
    scanf("%s%s",a+1,b+1);
    lena=strlen(a+1);
    lenb=strlen(b+1);
    for(R int i=1;i<=lena;i++)
    {
        int op=i&1;
        for(R int j=1;j<=lenb;j++)
        {
            if(a[i]==b[j])
                f[op][j]=f[op^1][j-1]+1;
            else
                f[op][j]=max(f[op^1][j],f[op][j-1]);
        }
    }
    printf("%d",f[lena&1][lenb]);
    return 0;
}

Longest Common Substring($LCS$)

标签：介绍   两种   因此   sub   str   end   gis   定义   math   

原文地址：https://www.cnblogs.com/-guz/p/9757012.html