红黑树分析清晰直白

时间：2018-10-13 16:49:24 阅读：163 评论：0 收藏：0 [点我收藏+]

标签：调整交流 bsp val util current 时间复杂度 nal 特征

概念

红黑树(Red-Block Tree)是一种近似平衡的二叉树,因此拥有较高的查询效率,但正因为是一棵近平衡树,因此在插入或删除节点时,会结构调整(变色,左旋,右旋),使其接近平衡,从而降低效率.
本文以TreeMap为例说明,TreeMap用红黑树构建,所以查询性能较高,时间复杂度为O(lgn),,而HashMap和LinkHashMap的时间复杂度都为O(n)(当hash不冲突时时间复杂度为O(1),但数量多起来后hash冲突显示不是我们能控制的,故写为O(n)),显然查询时比TreeMap耗时,关于时间复杂度分析,可移步到:时间复杂度分析理解

**重点:**红黑树拥有3特征,6种行为,行为的存在使得树在结构调整时,让树符合三种特征.这就是红黑树左旋,右旋,变色,原理,至于怎么设定的,就是发明者 Rudolf Bayer 的厉害的地方了.

特征:

1.根节点必须是黑色
2.红色节点不能连续(即红节点的父子节点都得是黑色)
3.对于每个节点,从该节点到树末梢(为null的节点),都有相同数量的黑色节点.
推导结论:一个节点到末端的最长路径不大于最小路径的2倍.

行为(就是源码(本文jdk1.8)的实现方式,6种情况):看下文结构调整.
红黑树样子: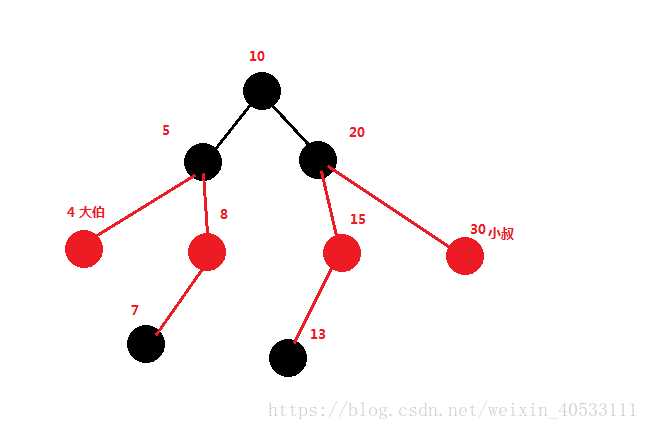
技术分享图片

正文:

get():
get(key)通过key查找,内部调getEntry(key),TreeMap每一个节点是一个Entry,有如下属性,可以像钩子一样构成一棵树.

  static final class Entry<K, V> implements java.util.Map.Entry<K,V{
        K key;
        V value;
        TreeMap.Entry<K, V> left;
        TreeMap.Entry<K, V> right;
        TreeMap.Entry<K, V> parent;
        boolean color = true;
    }

其中getEntry()方法做了些操作:支持两种比较器,如果在构造中传入比较器comparator则使用,否则使用默认实现的SortedMap中的comparator,通过key值进行比对,直至找到entry返回entry.value,否则为null.

 1  final TreeMap.Entry<K, V> getEntry(Object var1) {
 2         if (this.comparator != null) {
 3             return this.getEntryUsingComparator(var1);
 4         } else if (var1 == null) {
 5             throw new NullPointerException();
 6         } else {
 7             Comparable var2 = (Comparable)var1;
 8             TreeMap.Entry var3 = this.root;
 9 
10             while(var3 != null) {
11                 int var4 = var2.compareTo(var3.key);
12                 if (var4 < 0) {//向左
13                     var3 = var3.left;
14                 } else {
15                     if (var4 <= 0) {//找到了
16                         return var3;
17                     }
18 
19                     var3 = var3.right;//向右
20                 }
21             }
22 
23             return null;
24         }
25     }

put()

插入和删除操作是结构变动的原因,此处以插入说明.

 1  public V put(K var1, V var2) {
 2         TreeMap.Entry var3 = this.root;
 3         if (var3 == null) {
 4             this.compare(var1, var1);
 5             this.root = new TreeMap.Entry(var1, var2, (TreeMap.Entry)null);
 6             this.size = 1;
 7             ++this.modCount;
 8             return null;
 9         } else {
10             Comparator var6 = this.comparator;
11             int var4;
12             TreeMap.Entry var5;
13             if (var6 != null) {
14                 do {
15                     var5 = var3;
16                     var4 = var6.compare(var1, var3.key);
17                     if (var4 < 0) {
18                         var3 = var3.left;
19                     } else {
20                         if (var4 <= 0) {
21                             return var3.setValue(var2);
22                         }
23 
24                         var3 = var3.right;
25                     }
26                 } while(var3 != null);
27             } else {
28                 if (var1 == null) {
29                     throw new NullPointerException();
30                 }
31 
32                 Comparable var7 = (Comparable)var1;
33 
34                 do {
35                     var5 = var3;
36                     var4 = var7.compareTo(var3.key);
37                     if (var4 < 0) {
38                         var3 = var3.left;
39                     } else {
40                         if (var4 <= 0) {
41                             return var3.setValue(var2);
42                         }
43 
44                         var3 = var3.right;
45                     }
46                 } while(var3 != null);
47             }
48 
49             TreeMap.Entry var8 = new TreeMap.Entry(var1, var2, var5);
50             if (var4 < 0) {
51                 var5.left = var8;
52             } else {
53                 var5.right = var8;
54             }
55 
56             this.fixAfterInsertion(var8);//结构调整
57             ++this.size;
58             ++this.modCount;
59             return null;
60         }
61     }

插入分两步,第一步找位置,然后插入,没什么好说的,第二步是重点:结构调整.fixAfterInsertion方法如下:

 1 private void fixAfterInsertion(TreeMap.Entry<K, V> var1) {
 2         var1.color = false;
 3 
 4         while(var1 != null && var1 != this.root && !var1.parent.color) {
 5             TreeMap.Entry var2;
 6             if (parentOf(var1) == leftOf(parentOf(parentOf(var1)))) {//插入节点的父节点是爷爷节点的左节点
 7                 var2 = rightOf(parentOf(parentOf(var1))); //xi小叔节点
 8                 if (!colorOf(var2)) {
 9                     setColor(parentOf(var1), true);        //情况1
10                     setColor(var2, true);                        //:上色
11                     setColor(parentOf(parentOf(var1)), false);
12                     var1 = parentOf(parentOf(var1));        //获取爷爷节点,继续while中调整
13                 } else {
14                     if (var1 == rightOf(parentOf(var1))) {    //情况2
15                         var1 = parentOf(var1);//若x小叔节点是黑色或null,并且current插入的位置是右边,则左旋转,父节点变黑.......以下不再赘述
16                         this.rotateLeft(var1);
17                     }
18 
19                     setColor(parentOf(var1), true);        //情况3
20                     setColor(parentOf(parentOf(var1)), false);
21                     this.rotateRight(parentOf(parentOf(var1)));
22                 }
23             } else {
24                 var2 = leftOf(parentOf(parentOf(var1)));
25                 if (!colorOf(var2)) {
26                     setColor(parentOf(var1), true);    //情况4
27                     setColor(var2, true);
28                     setColor(parentOf(parentOf(var1)), false);
29                     var1 = parentOf(parentOf(var1));
30                 } else {
31                     if (var1 == leftOf(parentOf(var1))) {        //情况5
32                         var1 = parentOf(var1);
33                         this.rotateRight(var1);
34                     }
35 
36                     setColor(parentOf(var1), true);        //情况6
37                     setColor(parentOf(parentOf(var1)), false);
38                     this.rotateLeft(parentOf(parentOf(var1)));
39                 }
40             }
41         }
42 
43         this.root.color = true;
44     }

源码很清晰,调整的6种行为,主要通过三个手段,变色,左旋,右旋,交互使用,使得树最终满足三个特征.

**右旋图解示例:**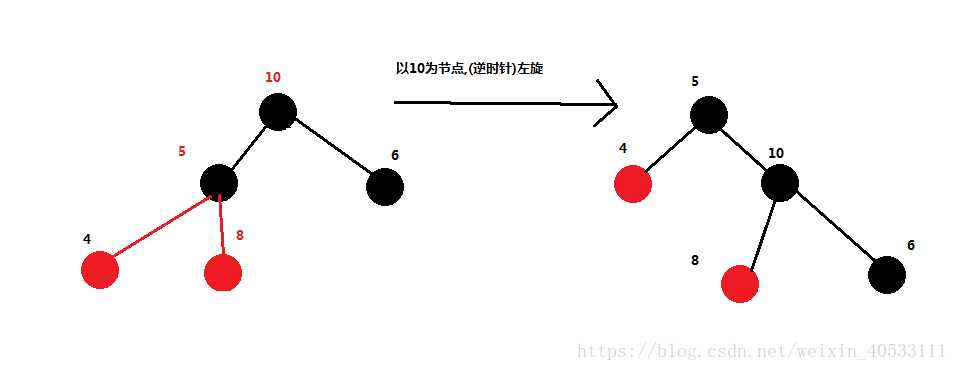
技术分享图片

**左旋图解示例:**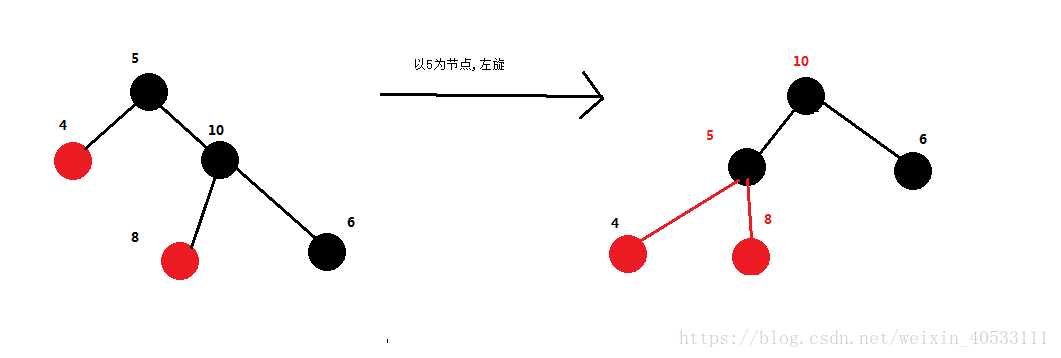
技术分享图片

|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

我不能保证理解都是对的和实践都是最佳的,这是个人的一些理解和实践,如发现问题,请联系笔者做出更改,交流->分享->进步.

认真工作,热爱生活.享受现在,拥抱未来~

|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

红黑树分析清晰直白

标签：调整交流 bsp val util current 时间复杂度 nal 特征

原文地址：https://www.cnblogs.com/leige109/p/9783181.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

红黑树分析 清晰直白

概念

特征:

正文:

红黑树分析清晰直白