标签:gre scale 离线 需要 standard scala ase 概念 矩阵
首先科普一下python里面对于数组的处理,就是如果获取数组大小,以及数组元素数量,这个概念是不一样的,就是一个size和len处理不用。老规矩,上代码:
1 arr2 = np.array([-19.51679711, -18.06166131, -16.65282549, 8.70287809,9.9485567 , 11.23867649, 3,4]) 2 pprint(arr2.size) 3 pprint(len(arr2))
>>8
>>8
貌似两者没啥区别,但是真的是这样吗?
Code:
1 arr2 = np.array([[-19.51679711, -18.06166131, -16.65282549, 8.70287809,9.9485567 , 11.23867649, 3,4]]) 2 pprint(arr2.size) 3 pprint(len(arr2))
>>8
>>1
在多维数组中,size代表的是所有的最小单元的总和,len则是代表多维数组元素的数量。
接着我们讲一下reshape,重新塑形,简单的讲就是将一个一维数组,打成多维数组:
1 arr = np.arange(6) 2 brr = arr.reshape((3,2)) 3 pprint(brr)
>> array([[0, 1], [2, 3], [4, 5]])
介绍完了基础知识,我们再来看一下SVM的分类学习
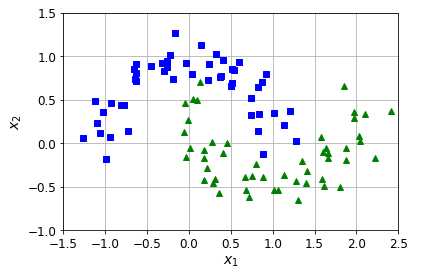
1 from sklearn.datasets import make_moons 2 X, y = make_moons(n_samples=100, noise=0.15, random_state=42) 3 4 def plot_dataset(X, y, axes): 5 plt.plot(X[y==0, 0], X[y==0, 1], "bs") 6 plt.plot(X[y==1, 0], X[y==1, 1], "g^") 7 plt.axis(axes) 8 plt.grid(True, which="both") #这个双引号行吗?没问题 9 plt.xlabel("$x_1$") 10 plt.ylabel("$x_2$") 11 12 plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) 13 plt.show()
1 from sklearn.pipeline import Pipeline 2 from sklearn.preprocessing import PolynomialFeatures 3 4 polynomial_svm_clf=Pipeline(( 5 ("ploy_feature", PolynomialFeatures(degree=3)), # 这里为什么需要多项式?有什么影响? 6 ("ploy_scale", StandardScaler()), # 缩小,减小离群点对于整体影响; 7 ("svm", LinearSVC(C=10, loss="hinge")) 8 )) 9 10 polynomial_svm_clf.fit(X, y)
1 # 基于坐标范围,形成点群(X)以及每个点的分类(y,等高线就是根据y值绘制的);所以可以看到每个点其实是有三个属性,坐标(x, y)以及分类 2 # 这个函数就是要生成这样的点,然后根据分类绘制等高线,这批套路非常重要 3 def plot_prediction(clf, axes): 4 x0s = np.linspace(axes[0], axes[1], 100) # 根据坐标范围等分点 5 x1s = np.linspace(axes[2], axes[3], 100) 6 # 这个是做什么的? meshgrid之后将会形成两套矩阵, 有大量容易,其实都是根据第一行(x0))和第一列(x1)进行衍生 7 x0, x1 = np.meshgrid(x0s, x1s) 8 # 这个又是在做什么?将衍生的矩阵里面的向量进行拉伸,通过np.c_进行整合,将会得到一个矩阵,矩阵里面每个向量都是两个元素(代表一个坐标), 9 # 来自于拉伸的两个矩阵的组合 10 X = np.c_[x0.ravel(), x1.ravel()] 11 plt.plot(X[501:600,0], X[501:600,1], "ys") 12 # 获取的完了predict为什么要reshape一下?clf.predict(X)返回的只是一个一维数组,每个数组对应X的一个向量(每个向量都是一个点), 13 # reshape之后,将会复制N行并返回N行的矩阵(N的值和X的行向量数量是一样的) 14 y_pred = clf.predict(X).reshape(x0.shape) 15 # decsion_function干嘛,为啥完事后有reshape一下?decision_function代表参数实例(各个元素)到分类平面(超平面)的距离,所以其数量 16 # 是等于X中向量的数量:10000,x0.shape是(100,100),于是reshape之后将会成为100行100列的多维数组 17 y_decision = clf.decision_function(X).reshape(x0.shape) 18 # 绘制分类(等高)线 19 plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2) 20 # 绘制距离线 21 plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1) 22 23 plot_prediction(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5]) #花了两条等高线 24 plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) # 换了两个交互的半环 25 plt.show()
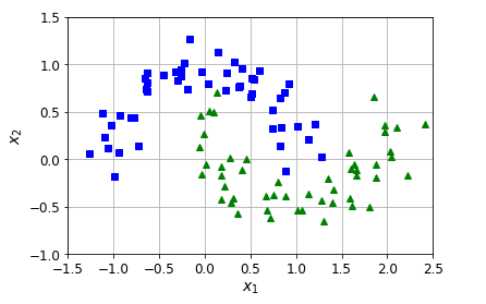
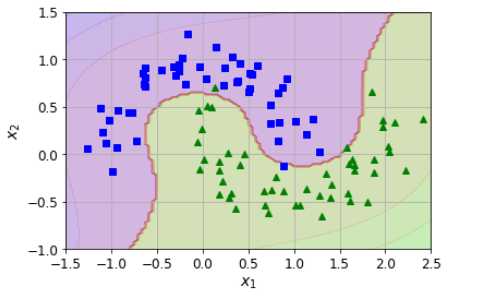
这段代码基本思路如下:
我先有数据,一个月牙环形数据(左侧图);然后我用这个数据,训练出来一个向量机(SVM),因为数据是曲线的,所以需要高次公式,于是搞了一个Pipeline,整合了Scalar和SVM来进行学习;通过fit函数,把模型的参数都搞掂了;然后我利用这个向量机来进行绘制边界线,怎么来绘制呢?首先在坐标中获取10000个点,均匀的散播在整个坐标系中;我再把这些点扔到SVM中,让他根据之前学习的结果获取分类,contours英文意思就是轮廓,在matlibplot中,contourf这个函数将会把轮廓画出来,并且填充颜色;简单讲就是同类别同颜色,然后会在不同类别之间画出一条分界线。
这段代码意义在于讲清楚了SVM的学习能力;通过针对半月环形数据的学习掌握了参数,具备了对于点判断分类的能力;未来当有海量的数据需要判断的时候,会基于之前的学习模型,来进行判断,分类,在右图海量数据作为测试数据的场景下,通过轮廓线说明了SVM所具备的学习能力。
标签:gre scale 离线 需要 standard scala ase 概念 矩阵
原文地址:https://www.cnblogs.com/xiashiwendao/p/9787260.html