标签：public   ref   distance   思路   www   amp   png   har   out   

描述

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace ‘h‘ with ‘r‘)
rorse -> rose (remove ‘r‘)
rose -> ros (remove ‘e‘)

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove ‘t‘)
inention -> enention (replace ‘i‘ with ‘e‘)
enention -> exention (replace ‘n‘ with ‘x‘)
exention -> exection (replace ‘n‘ with ‘c‘)
exection -> execution (insert ‘u‘)

思路：动态规划

这是一个经典的动态规划问题，思路参考斯坦福的课程：http://www.stanford.edu/class/cs124/lec/med.pdf

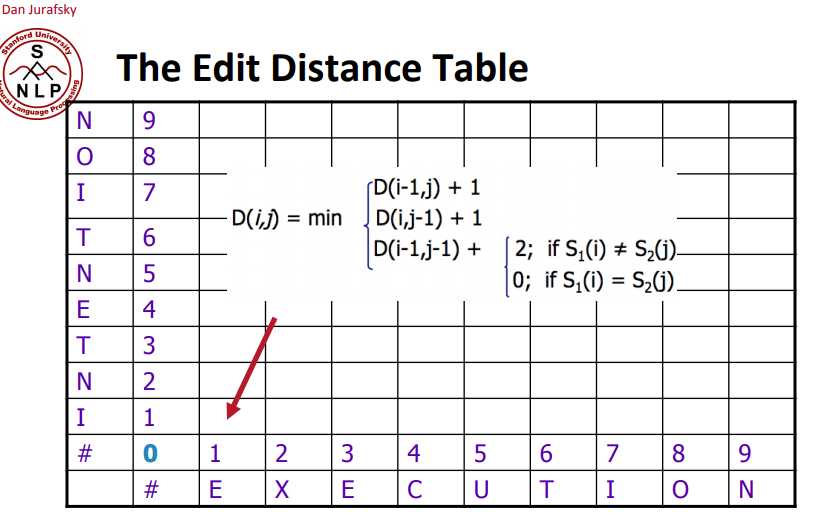
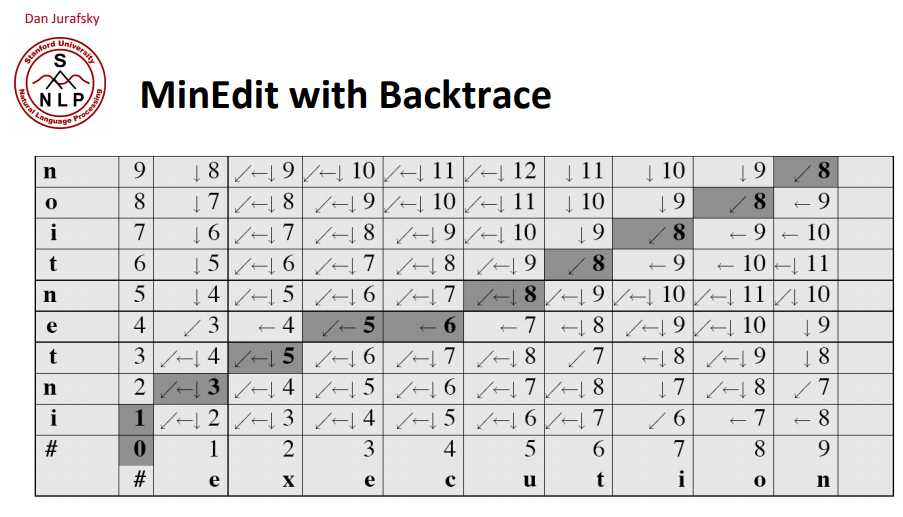
这里把加2变成加1即可

1. dp[i][0] = i;
2. dp[0][j] = j;
3. dp[i][j] = dp[i - 1][j - 1], if word1[i - 1] = word2[j - 1];
4. dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j] + 1, dp[i][j - 1] + 1), otherwise.

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int> > dp(m+1, vector<int>(n+1, 0));
        for(int i = 1;i<=m;++i)
            dp[i][0] = i;
        for(int i = 1;i<=n;++i)
            dp[0][i] = i;
        for(int i = 1;i<=m;++i){
            for(int j = 1;j<=n;++j){
                if(word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = min(dp[i-1][j-1], min(dp[i][j-1], dp[i-1][j])) + 1;
            }
        }
        return dp[m][n];
    }
};

【LeetCode】【动态规划】Edit Distance

标签：public   ref   distance   思路   www   amp   png   har   out   

原文地址：https://www.cnblogs.com/ygh1229/p/9798807.html