标签:port turn dice neu class rdp info red 初始
tensorflow基础暂不介绍
pip install seaborn
安装 matplotlib:
pip install matplotlib
安装 python3-tk:
sudo apt-get install python3-tk -y
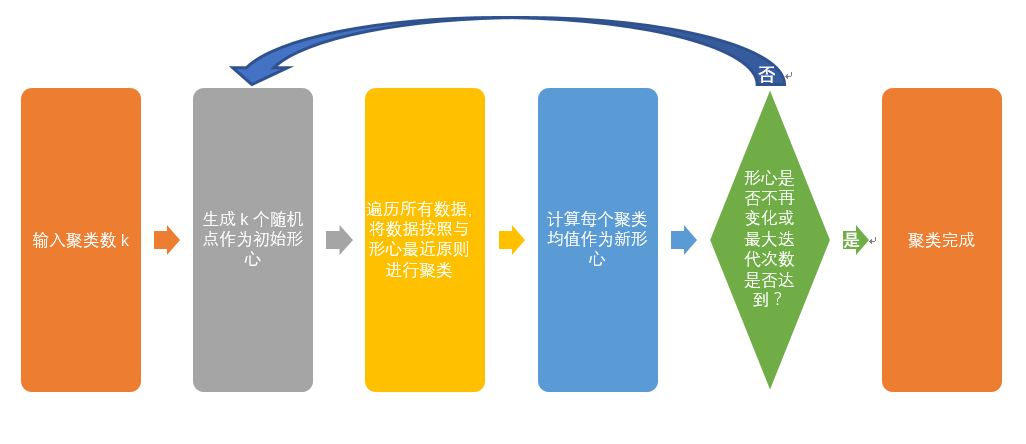
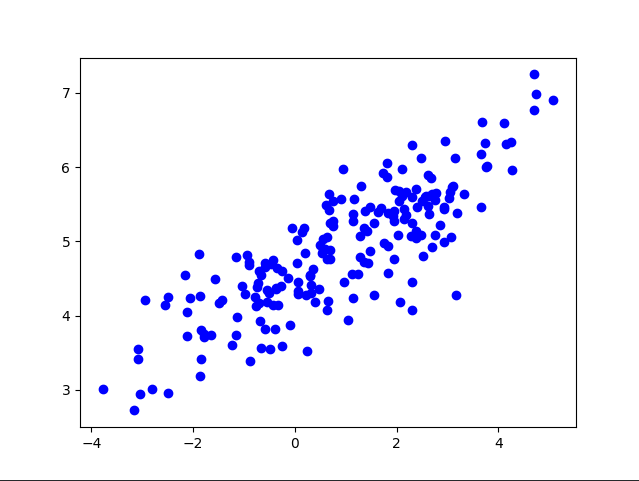
200个数据进行 K-Means 聚类,首先我们先来了解一些生成的测试数据的形式代码:
# -*- coding: utf-8 -*- import matplotlib matplotlib.use(‘Agg‘) import numpy as np from numpy.linalg import cholesky import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import tensorflow as tf from random import choice, shuffle from numpy import array def KMeansCluster(vectors, noofclusters): noofclusters = int(noofclusters) assert noofclusters < len(vectors) #找出每个向量的维度 dim = len(vectors[0]) #辅助随机地从可得的向量中选取形心 vector_indices = list(range(len(vectors))) shuffle(vector_indices) #计算图 graph = tf.Graph() with graph.as_default(): #计算的会话 sess = tf.Session() ########从现有的点集合中抽取出一部分作为默认的中心点######## centroids = [tf.Variable((vectors[vector_indices[i]])) for i in range(noofclusters)] centroid_value = tf.placeholder("float64", [dim]) cent_assigns = [] for centroid in centroids: cent_assigns.append(tf.assign(centroid, centroid_value)) assignments = [tf.Variable(0) for i in range(len(vectors))] assignment_value = tf.placeholder("int32") cluster_assigns = [] for assignment in assignments: cluster_assigns.append(tf.assign(assignment, assignment_value)) #############下面创建用于计算平均值的操作节点############# mean_input = tf.placeholder("float", [None, dim]) mean_op = tf.reduce_mean(mean_input, 0) #################用于计算欧氏距离的节点################# v1 = tf.placeholder("float", [dim]) v2 = tf.placeholder("float", [dim]) euclid_dist = tf.sqrt(tf.reduce_sum(tf.pow(tf.subtract( v1, v2), 2))) centroid_distances = tf.placeholder("float", [noofclusters]) cluster_assignment = tf.argmin(centroid_distances, 0) ###################初始化所有的状态值################### init_op = tf.global_variables_initializer() sess.run(init_op) #######################集群遍历####################### #接下来在 K-Means 聚类迭代中使用最大期望算法,简单起见最大迭代次数直接设置为30次 noofiterations = 30 for iteration_n in range(noofiterations): #####################期望步骤##################### #首先遍历所有的向量 for vector_n in range(len(vectors)): vect = vectors[vector_n] #计算给定向量与分配的形心之间的欧氏距离 distances = [sess.run(euclid_dist, feed_dict={ v1: vect, v2: sess.run(centroid)}) for centroid in centroids] #下面可以使用集群分配操作,将算出的距离当做输入 assignment = sess.run(cluster_assignment, feed_dict = { centroid_distances: distances}) #接下来为每个向量分配合适的值 sess.run(cluster_assigns[vector_n], feed_dict={ assignment_value: assignment}) ####################最大化的步骤#################### #基于上述的期望步骤,计算每个新的形心的距离从而使集群内的平方和最小 for cluster_n in range(noofclusters): #收集所有分配给该集群的向量 assigned_vects = [vectors[i] for i in range(len(vectors)) if sess.run(assignments[i]) == cluster_n] #计算新的集群形心 new_location = sess.run(mean_op, feed_dict={ mean_input: array(assigned_vects)}) #为每个向量分配合适的形心 sess.run(cent_assigns[cluster_n], feed_dict={ centroid_value: new_location}) #返回形心和分组 centroids = sess.run(centroids) assignments = sess.run(assignments) return centroids, assignments ############生成随机测试数据############### sampleNo = 200;#生成数据数量 mu =3 # 数据遵从二维正态分布 mu = np.array([[1, 5]]) Sigma = np.array([[1, 0.5], [1.5, 3]]) R = cholesky(Sigma) srcdata= np.dot(np.random.randn(sampleNo, 2), R) + mu plt.plot(srcdata[:,0],srcdata[:,1],‘bo‘) plt.savefig(‘data.png‘) ############ kmeans 算法计算############### k=4 center,result=KMeansCluster(srcdata,k) print (center) ############利用 seaborn 画图############### res={"x":[],"y":[],"kmeans_res":[]} for i in range(len(result)): res["x"].append(srcdata[i][0]) res["y"].append(srcdata[i][1]) res["kmeans_res"].append(result[i]) pd_res=pd.DataFrame(res) sns.lmplot("x","y",data=pd_res,fit_reg=False,size=5,hue="kmeans_res") plt.show() plt.savefig(‘kmeans.png‘)


参考:https://codesachin.wordpress.com/2015/11/14/k-means-clustering-with-tensorflow/
标签:port turn dice neu class rdp info red 初始
原文地址:https://www.cnblogs.com/fclbky/p/9802938.html