标签:start ima 后序 initial bin failure 存在 ini count
优点:代码思路简单,很多书籍上直接给出。
缺点:需多个方式(先序+中序或先序+后序)才能判别出
优点:直接显现,错误一看便知
缺点:代码思路较难,新手难以控制
树的各种遍历许多书籍已经给出,我的个人博客上也有一些版本,网上的版本也大都一致。这里不再叙述
下面介绍一种本人原创的一种思路:
首先这种想法需要一个另外的结构数组来保存你的树节点
假如有一棵树为下图所示:
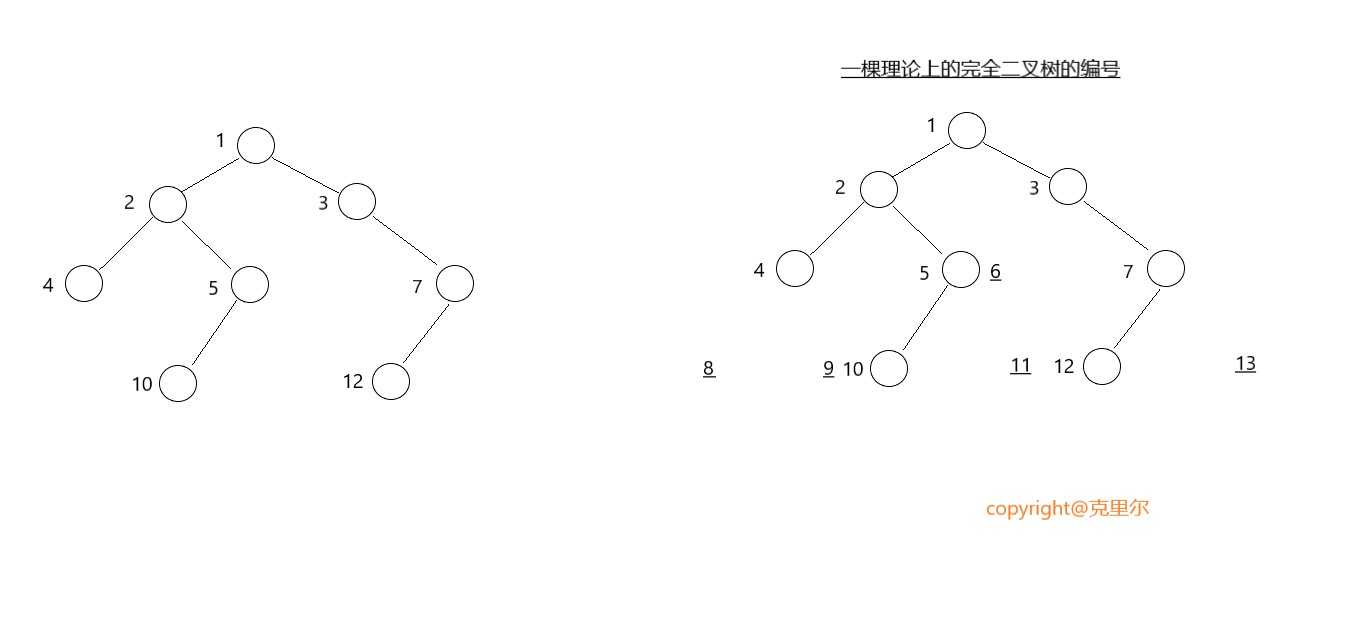
由上图可知要想打印一颗比较直观的二叉树,我们最主要的就是要考虑那些理论完全二叉树上没有节点的地方如何控制输出如上图右边的(5,7,8,9,11,12,13)节点上是空的这个时候我们应该用空格
或者其他自定义的字符来表示这个空节点
下面给出代码:
DisplayTree.c:
#include"BinaryTree.h" //按需选择自己需要打印的各种类型树; //但只支持类似下面树结点的申明形式: //struct TreeNode //{ // TreeElementType Element; // struct TreeNode *Left; // struct TreeNode *Right; //}; #include<stdio.h> #include<stdlib.h> #include<math.h> /* 函数功能:直观打印二叉树 实现函数功能的封装性; 本函数主要思想是给二叉树结点做顺序序号标记; 封装完好,增强了功能性。 */ typedef BinTree Tree;//打印其他树类型,请修改此处树类型指针 struct FlagNode { TreeElementType Element; int Sign; }; typedef struct FlagNode *Flag; static int count = 0; Flag Initialize(int ArraySize); void MarkTreeNode(Tree T, Flag Array, int f); void PrintFlag(Flag Array, int ArraySize); void PrintBinaryTree(Flag Array, int ArraySize, int DepthOfTree); /*下列函数按需选择*/ //int SumNode(Tree T); //int Depth(Tree T); void TreePrint(Tree T) { int i = 1;//从1号开始标记 int NumberOfTreeNode = SumNode(T); int DepthOfTree = Depth(T); // printf("DepthOfTree = %d\n", DepthOfTree); // printf("NumberOfTreeNode = %d\n", NumberOfTreeNode); Flag A; A = Initialize(NumberOfTreeNode); //这里放一组深度为5的满二叉树元素组:phdba00c00fe00g00lji00k00nm00o00xtrq00s00vu00w00bzy00a00dc00e00 MarkTreeNode(T, A, i); // PrintFlag(A, NumberOfTreeNode); printf("The binary tree is look like:\n"); PrintBinaryTree(A, NumberOfTreeNode, DepthOfTree); } Flag Initialize(int ArraySize) { int i; Flag Array;//申请树的元素个数 Array = (Flag)malloc(sizeof(struct FlagNode) * ArraySize); if(NULL == Array) { printf("Allocation failure!"); return NULL; } return Array; } //给树结点做标记,按理论完全二叉树的序号标记 void MarkTreeNode(Tree T, Flag Array, int f) { if(NULL != T) { Array[count].Sign = f; Array[count].Element = T->Element; count++; MarkTreeNode(T->Left, Array, f * 2); MarkTreeNode(T->Right, Array, f * 2 + 1); } } void PrintFlag(Flag Array, int ArraySize) { int i; for(i = 0; i < ArraySize; i++) printf("%c-->%d\n", Array[i].Element, Array[i].Sign); } void PrintBinaryTree(Flag Array, int ArraySize, int DepthOfTree) { int Line;//行数 int PerLineNode;//理论每行结点总数 int LineStart;//理论完全二叉树的第一个结点序号 int Blank = DepthOfTree; for(Line = 1; Line <= DepthOfTree; Line++)//此循环控制打印的行数 { int i; /*下面得for循环控制输出每行前面得空格*/ for(i = 0; i < pow(2, Blank - 1); i++) printf(" "); printf("\b"); PerLineNode = pow(2, Line - 1); /*理论上每行的第一个结点序号也是该行的理论总结点数(如下图)*/ /* 1 */ /* 2 3 */ /* 4 5 6 7 */ for(LineStart = PerLineNode; LineStart < PerLineNode * 2; LineStart++) { /*下面代码识别从LineStart从开始到末尾的序号是否存在结点,不存在则输出" "*/ int exist = 0; for(i = 0; i < ArraySize; i++) { if(LineStart == Array[i].Sign) { printf("%c", Array[i].Element); exist = 1; } } if(exist == 0) printf(" "); /*下面for循环控制输出每个理论存在结点得后得空格数*/ for(i = 0; i < pow(2, Blank); i++) printf(" "); printf("\b");//回退一格,具体细节可画图 } printf("\n"); Blank--; } } //下列两个函数根据树的操作可选 //int Depth(Tree T)//输出的是整个二叉树的深度 //{ // int DepthOfLeft = 0; // int DepthOfRight = 0; // if(NULL == T) // return 0; // else // { // DepthOfLeft = Depth(T->Left); // DepthOfRight = Depth(T->Right); // return (DepthOfLeft > DepthOfRight) ? DepthOfLeft + 1 : DepthOfRight + 1; // } //} //int SumNode(Tree T) //{ // if(NULL == T) // return 0; // else if(T->Left == NULL && T->Right == NULL) // return 1; // else // return SumNode(T->Left) + SumNode(T->Right) + 1;//加1等于是每次返回 加一个根结点 //}
下面是我的一组简单测试:
test.c:
#include"PrintTree.c" #include"TreeOperate.c" #include<stdio.h> #include<stdlib.h> int main() { BinTree BT; BT = IterationCreateTree(); TreePrint(BT); return 0; }
输出图样:

标签:start ima 后序 initial bin failure 存在 ini count
原文地址:https://www.cnblogs.com/Crel-Devi/p/9803238.html