标签:info lse 二维 获取元素 inf png 优化 return 思路
一、题目
1、审题
2、分析
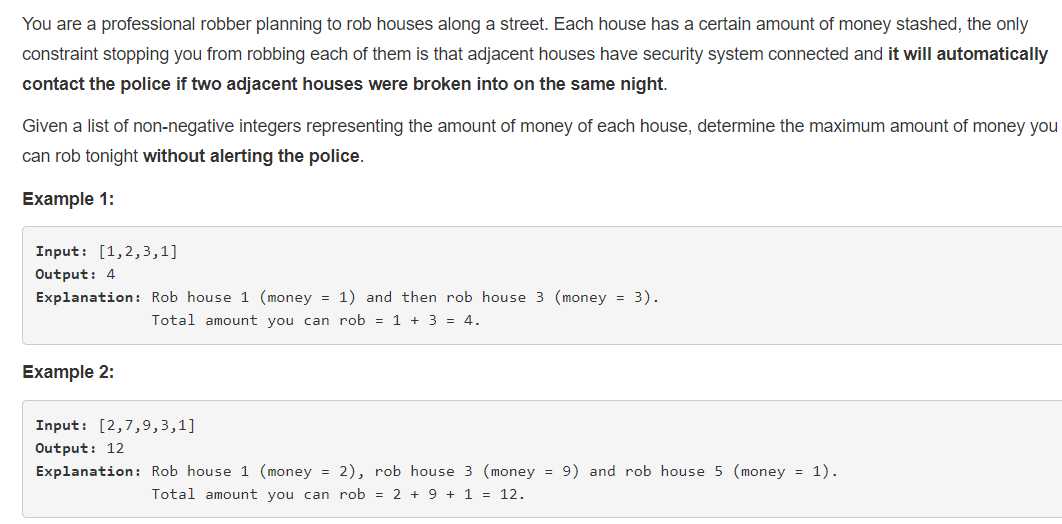
给出一个整形数组,你不能获取连续元素,只能间隔获取元素的值,求你能获取的元素的和的最大值为多大。
二、解答
1、思路:
方法一、
采用两个变量 max1、max2 记录奇数、偶数位置所能获取的最大值。
可能获取此位置的值,也可能不获取。
public int rob(int[] nums) { int max1 = 0, max2 = 0; for (int i = 0; i < nums.length; i++) { if(i % 2 == 0) max1 = Math.max(max1 + nums[i], max2); else max2 = Math.max(max1, max2 + nums[i]); } return Math.max(max1, max2); }
方法二、
采用一维动态数组记录当前位置能获取的最大值。
public int rob2(int[] nums) { int len = nums.length; if(len == 1) return nums[0]; int[] dp = new int[len]; dp[0] = nums[0]; dp[1] = Math.max(nums[0], nums[1]); for (int i = 2; i < len; i++) dp[i] = Math.max(dp[i-2] + nums[i], dp[i-1]); return dp[len - 1]; }
方法三、
采用一个二维数组记录当前位置能获取的最大值。
dp[i][1]: 表示获取第 i 个元素的值;
dp[i][0]:表示不获取第 i 个元素的值。
public int rob3(int[] nums) { int len = nums.length; int[][] dp = new int[len + 1][2]; for (int i = 1; i <= len; i++) { dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1]); dp[i][1] = nums[i - 1] + dp[i - 1][0]; } return Math.max(dp[len][0], dp[len][1]); }
优化:
可以简化为用两个变量代替动态数组。
public int rob4(int[] nums) { int curNo = 0; int curYes = 0; for(int num: nums) { int prevNO = curNo; curNo = Math.max(curNo, curYes); curYes = num + prevNO; } return Math.max(curNo, curYes); }
标签:info lse 二维 获取元素 inf png 优化 return 思路
原文地址:https://www.cnblogs.com/skillking/p/9807475.html