标签:题解 The turn height scanf format bsp main script
Problem Description
Given a number N, you are asked to count the number of integers between A and B inclusive which are relatively prime to N.
Two integers are said to be co-prime or relatively prime if they have no common positive divisors other than 1 or, equivalently, if their greatest common divisor is 1. The number 1 is relatively prime to every integer.
Input
The first line on input contains T (0 < T <= 100) the number of test cases, each of the next T lines contains three integers A, B, N where (1 <= A <= B <= 1015) and (1 <=N <= 109).
Output
For each test case, print the number of integers between A and B inclusive which are relatively prime to N. Follow the output format below.
Sample Input
Sample Output
Case #1: 5
Case #2: 10
Hint
In the first test case, the five integers in range [1,10] which are relatively prime to 2 are {1,3,5,7,9}.
解题思路:求区间[A,B]与N互质的数的个数,我们可以从其对立面来考虑:分别求区间[1,A-1]、区间[1,B]中与N不互质的数的个数为num1、num2,那么区间[A,B]与N互质的数的个数就有(B-num2)-(A-1-num1)。怎么求区间与N不互质的数的个数呢?先分解出N的所有素因子,因为任何一个不小于2的数都能表示成若干个素数的乘积,然后用其素因子来筛选计算出区间中与N不互质的数的个数即X/p_i(p_i为素因子),这里要用容斥定理,不重复计数,也没有遗漏,公式: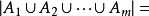
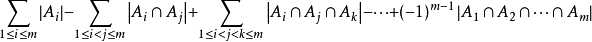
AC代码:
1 #include<bits/stdc++.h>
2 using namespace std;
3 typedef long long LL;
4 int t,cnt,prime[15];LL a,b,n;
5 LL solve(LL x){//求与n不互质的总个数
6 int num;LL ans=0,tp;
7 for(int i=1;i<(1<<cnt);++i){//用二进制来表示每个质因子是否被使用,即有2^cnt-1种可能,此时cnt较小,题目中1e9最多也就8个素因子,二进制优化
8 tp=1,num=0;
9 for(int j=0;j<cnt;++j)
10 if(i&(1<<j))num++,tp*=prime[j];//表示选择哪几个素因子
11 if(num&1)ans+=x/tp;//奇加
12 else ans-=x/tp;//偶减
13 }
14 return x-ans;
15 }
16 int main(){
17 while(~scanf("%d",&t)){
18 for(int i=1;i<=t;++i){
19 scanf("%lld%lld%lld",&a,&b,&n);cnt=0;
20 for(LL j=2;j*j<=n;++j){//求出n内的所有质因子
21 if(n%j==0){
22 prime[cnt++]=j;
23 while(n%j==0)n/=j;
24 }
25 }
26 if(n>1)prime[cnt++]=n;
27 printf("Case #%d: %lld\n",i,solve(b)-solve(a-1));//区间差
28 }
29 }
30 return 0;
31 }
题解报告:hdu 4135 Co-prime(容斥定理入门)
标签:题解 The turn height scanf format bsp main script
原文地址:https://www.cnblogs.com/acgoto/p/9814342.html