883. Projection Area of 3D Shapes

标签：==   hat   sum   tin   ons   Dimension   shadow   inpu   rom   

On a N * N grid, we place some 1 * 1 * 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).

Now we view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3 dimensional figure to a 2 dimensional plane.

Here, we are viewing the "shadow" when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Example 1:

Input: [[2]]
Output: 5

Example 2:

Input: [[1,2],[3,4]]
Output: 17
Explanation:
Here are the three projections ("shadows") of the shape made with each axis-aligned plane.

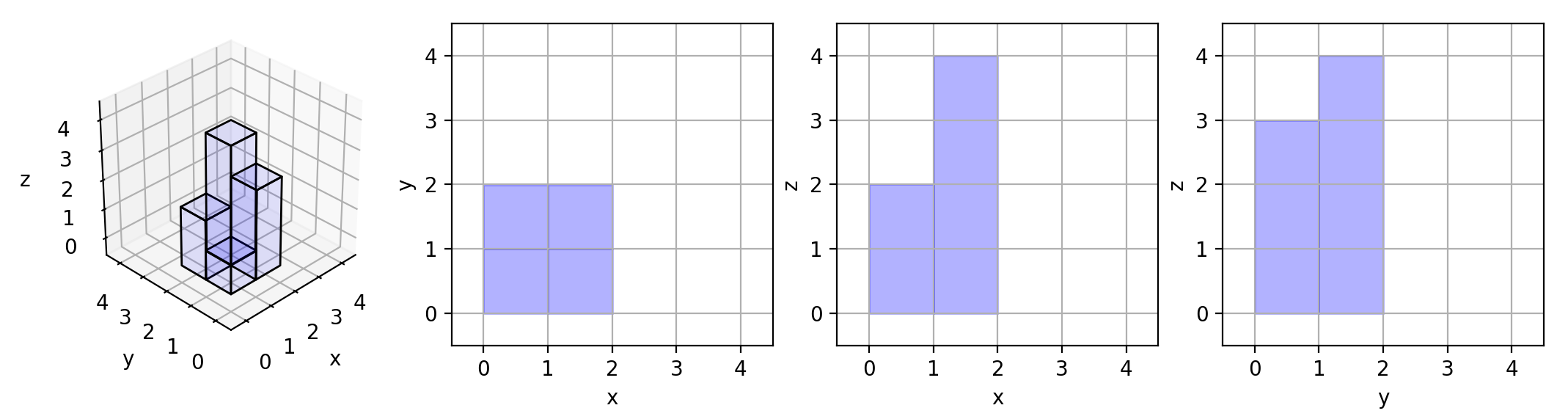
Example 3:

Input: [[1,0],[0,2]]
Output: 8

Example 4:

Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 14

Example 5:

Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 21

Note:

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 50

class Solution:
    def projectionArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        front = [0] * len(grid)
        side = [0] * len(grid)
        top = 0
        for i in range(len(grid)):
            for j in range(len(grid[i])):
                if grid[i][j] == 0:
                    continue
                top += 1
                front[i] = max(front[i],grid[i][j])
                side[j] = max(side[j],grid[i][j])
        return top + sum(front) + sum(side)

883. Projection Area of 3D Shapes

标签：==   hat   sum   tin   ons   Dimension   shadow   inpu   rom   

原文地址：https://www.cnblogs.com/bernieloveslife/p/9813172.html