标签：放松 建模 splay 最小值 机器 不同 尺度 分类 了解
对于线性可分的数据而言，我们采用PLA算法也能得到想要分类的效果，但是数据进入的顺序不同，那么得到的分类效果也有所区别，如图1.1所示。我们希望能够找到一条鲁棒性最好的线来对问题进行分类。那么，我们就开始了对这个问题的建模过程了。
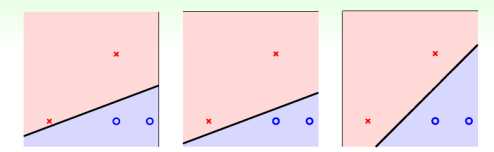
图1.1
step1:
用自然语言来表示我们的算法。我们当然希望最终找到的线与所有样本点距离最小值最大，而且这条线要将所有的样本点完全正确分类，写成数学语言就是这样的：
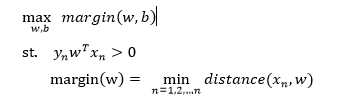
step2:
我们可以将计算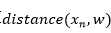
用明确的距离公式来替代：
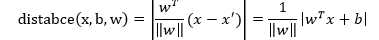
这样，我们的算法就改写成了下面的式子：
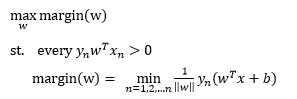
step3:
上面的式子对于求解来说还是太过困难，于是我们对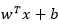
进行一些尺度变化，原因是尺度变化并不会影响分类的效果。简单起见，我们就让与分类面最近的点的满足
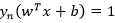（对于一组确定
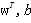的而言，同时在这组确定的下，其他数据点一定满足
）。
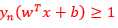因此，可以获得模型：
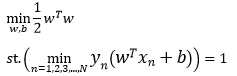
更近一步，缩放条件更有利于问题的规划求解，而且不会使解落到原问题之外，所以我们将条件放松一点。
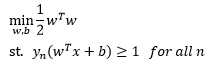
step4:
问题已经变成了解决二次规划（QP）了。
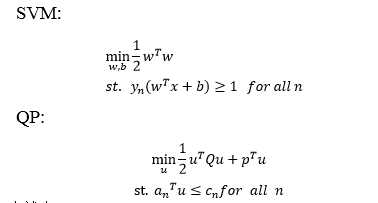
对应起来就有：
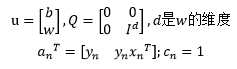
总结： 线性SVM减少了VC维的数量，从而让机器学习模型具有更好的泛化能力（Ein≈Eout），再引入非线性变化就会提升SVM训练样本让Ein≈0。
标签：放松 建模 splay 最小值 机器 不同 尺度 分类 了解
原文地址：https://www.cnblogs.com/hustyan/p/9826173.html
