标签：swa   init   cos   class   sum   完整   name   进制   .com   

快速傅里叶变换(FFT)

挂个博客
主要思想:分治
主要用途:优化两个多项式相乘的时间复杂度\((O(n^2)->O(nlogn))\)

前置

对于一个多项式\[A(x)=\sum_{i=0}^{n-1}a_ix^i\]把它看成函数,有\(y_k=A(x_k)\),图像上的点\((x_k,y_k)\)
定理:给你\(n\)个不同的点,一定有唯一的\(n\)次多项式\(A(x)\)
两个点相乘的复杂度是\(O(1)\)的
现在考虑指定多项式\(a,b\)中各n个点的横坐标,求出它们的纵坐标(求值),
再乘起来得到新的\(n\)个点,计算\(a,b\)的乘积\(c\)(插值)
先不管插值,求值还是\(O(n^2)\)的
于是我们要选择一些鬼畜的横坐标加速求值过程,

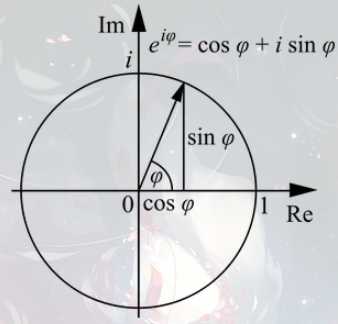
也就是\(n\)次单位根\(w\),满足\(w^n=1\),发现它在复数域中恰好有\(n\)个,且都在一个单位圆上
\[w_n^k=e^{2πki/n}\]
其中\(w_n^1=e^{2πi/n}=cos(2π/n)+i\) \(sin(2π/n)\)是主\(n\)次单位根(之后简写为\(w_n\)),
所有其它\(n\)次单位根都是它的整次幂
三大引理
消去引理:\[w_{dn}^{dk}=w_n^k\]
证明:\[w_{dk}^{dn}=e^{2dkπi/dn}=w_n^k\]
折半引理:\[(w_n^{k+n/2})^2=(w_n^k)^2\]
证明:\[(w_n^{k+n/2})^2=w_n^{2k+n}=w_n^nw_n^{2k}=(w_n^k)^2\]
其中\(w_n^n=cos2π+i\) \(sin2π=1\)

求和引理:
对于任意整数\(n≥1\)与不能被\(n\)整除的非负整数\(k\),有:
\[\sum_{j=0}^{n-1}(w_n^{k})^j=0\]
证明:\[S=(w_n^k)^0+(w_n^k)^1+...+(w_n^k)^{n-1}\]
\[w_n^kS=(w_n^k)^1+(w_n^k)^2+...+(w_n^k)^n\]
\[S=(w_n^k)^n-(w_n^k)^0/w_n^k-1=0\]

高能

DFT定义
对于多项式\(A\)的系数表达\(\vec{a}=(a_0,a_1,...,a_{n?1})\)
定义\[y_k=A(w_n^k)=\sum_{i=0}^{n-1}a_i(w_n^k)^i\]
则\(\vec{y}=(y_0,y_1,...,y_{n?1})\)就是\(\vec{a}\)的离散傅里叶变换
记作\(\vec{y}=DFT_n(\vec{a})\)
FFT求值
\[A(x)=\sum_{i=0}^{n-1}a_ix^i\]原多项式
\[A^{[0]}(x)=a_0+a_2x+...+a_{n-2}x^{n/2-1}\]\[A^{[1]}(x)=a_1+a_3x+...+a_{n-1}x^{n/2-1}\]姑且叫它子多项式

可以看出\(A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)\),相当于原多项式按照下标奇偶被拆开
此时问题变成了求\(x=(w_n^k)^2\)时\(A^{[0]}(x)\)和\(A^{[1]}(x)\)的值\((k=0,1,...,n-1)\)
根据折半引理,有\[(w_n^1)^2=w_n^2=w_{n/2}^1\]\[(w_n^{n-1})^2=w_n^{-2}(w_n^n)^2=w_n^{n-2}=w_{n/2}^{n/2-1}\]其实要求的\(x=(w_{n/2}^k)(k=0,1,...,n/2-1)\)
由此我们将问题的\(size\)减半,将\(DFT_n\)拆成两个\(DFT_{n/2}\)来做,一直递归下去
直到\(size\)=1时,\(y_0=a_0w_1^0=a_0\),求值的复杂度变为O(nlogn)
具体做法的话,设\(\vec{y^{[0]}}=A^{[0]}(x)\)的\(DFT\)结果,\(\vec{y^{[1]}}=A^{[1]}(x)\)的\(DFT\)结果
下述都有\(k=(0,1,...,n/2-1)\)
对于前半部分\[y^{[0]}_k=A^{[0]}(w^k_{n/2})=A^{[0]}(w^{2k}_n)\] \[y^{[1]}_k=A^{[1]}(w^k_{n/2})=A^{[1]}(w^{2k}_n)\] \[y_k=y^{[0]}_k+w_n^ky^{[1]}_k\]
对于后半部分\[y_{k+n/2}=y^{[0]}_{k+n/2}+w_n^{k+n/2}y^{[1]}_{k+n/2}\] 由于\(w_n^{k+n/2}=w_2^1w_n^k=e^{πi}w_n^k=(cosπ+i\) \(sinπ)w_n^k=-w_n^k\)
有\[y_{k+n/2}=y^{[0]}_{k+n/2}-w_n^ky^{[1]}_{k+n/2}\]
因此我们可以用变量存储\(w_n^k\),减少运算量
至于\(w_n\)的幂次,我们也是选择迭代计算降低复杂度
FFT插值
但插值的复杂度还是不对,我们将\(DFT\)写成矩阵乘积的形式\(\vec{y}=V_n\vec{a}\)

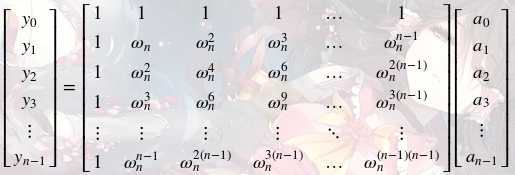
对于它的逆运算,选择\(\vec{a}=DFT^{-1}(\vec{y})\)
求出它的逆矩阵\(V_n^{-1}\),一个矩阵与其逆矩阵之积为一个\(n*n\)的单位矩阵
定理\[[V_n^{-1}]_{ij}=w_n^{-ij}/n\]
证明
考虑\(V_n*V_n^{-1}\)在\((i,j)\)的元素值,根据求和引理
\[[V_nV_n^{-1}]_{ij}=\sum_{k=0}^{n-1}(w_n^{-ki}/n)(w_n^{kj})=\sum_{k=0}^{n-1}w_n^{k(j-i)}/n\]当\(i=j\)时,\([V_nV_n^{-1}]_{ij}=\sum_0^{n-1}w_n^0/n=\sum_0^{n-1}e^0/n=1\)
否则\([V_nV_n^{-1}]_{ij}=0\),命题得证
我们发现它和\(DFT\)的定义极其相似!唯一的区别仅仅在于前面的多出的\(1/n\)和\(w_n\)指数上多出来的负号,也就是说,我们可以通过稍微修改一下\(FFT\)就可以用来计算\(DFT^{?1}\)了!
至此你已经可以在理论\(O(nlogn)\)的光环下写出\(FFT\)了

优化

递归常数好像有点大
那就递推!!!,从一个节点的算起,每次合并两个,直到算完整个多项式
但是每次合并哪两个呢?
找一找规律

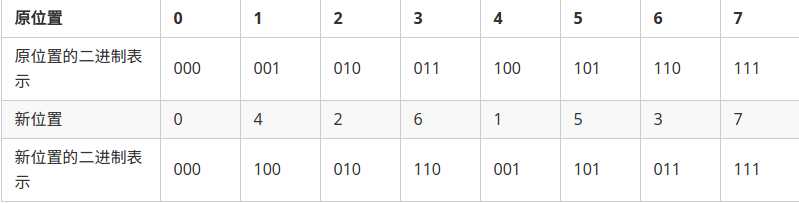
\(TM\)竟然是把二进制逆了个序?!!
\(init\)出每个下标逆序后的数,合并相邻两个(详细见代码)

就没了?!!!

#define il inline
#define ri register int
#define de double
#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int N=3e6+5;
const de Pi=acos(-1.0);
il int re(){
    ri x=0,w=1;register char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}
int n,m,l,s=1,r[N];
struct complex{
    de x,y;
    complex (de xx=0,de yy=0){x=xx,y=yy;}
}a[N],b[N];
complex operator +(complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b){
    return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}
il void fft(complex A[],ri op){
    for(ri i=0;i<s;i++)
        if(i<r[i])swap(A[i],A[r[i]]);//按奇偶分组
    for(ri i=1;i<s;i<<=1){//枚举区间的半长(即k/2)
        complex wn(cos(Pi/i),op*sin(Pi/i));//主n次单位根
        for(ri len=(i<<1),j=0;j<s;j+=len){//len为区间长
            complex w(1,0);
            for(ri k=0;k<i;k++,w=w*wn){//分组处理每个小区间
                complex x=A[j+k],y=w*A[j+i+k];
                A[j+k]=x+y;
                A[j+i+k]=x-y;
            }
        }
    }
}
int main(){
    n=re(),m=re();
    for(ri i=0;i<=n;i++)a[i].x=re();
    for(ri i=0;i<=m;i++)b[i].x=re();
    while(s<=n+m)s<<=1,l++;
    for(ri i=0;i<s;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));//处理出逆序后的数
    fft(a,1);
    fft(b,1);//求值
    for(ri i=0;i<=s;i++)a[i]=a[i]*b[i];//相乘
    fft(a,-1);//插值
    for(ri i=0;i<=n+m;i++)
        printf("%d ",(int)(a[i].x/s+0.5));//+0.5防掉精度(记得要/s)
    return 0;
}

快速傅里叶变换(FFT)

标签：swa   init   cos   class   sum   完整   name   进制   .com   

原文地址：https://www.cnblogs.com/sdzwyq/p/9833674.html