数据结构之二叉树

标签：span   img   n+1   取整   树根   后序   分享   先序   深度   

参考博客：

https://blog.csdn.net/qq_40772692/article/details/79343914

一、二叉树的常用性质

<1>.在二叉树的第i层上最多有2 i-1 个节点 。（i>=1）

<2>.二叉树中如果深度为k(有k层),那么最多有2k-1个节点。(k>=1）

<3>.若二叉树按照从上到下从左到右依次编号，则若某节点编号为k，则其左右子树根节点编号分别为2k和2k+1;

<4>.二叉树分类：满二叉树，完全二叉树

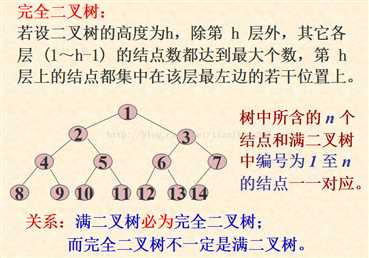
<5>.在完全二叉树中，具有n个节点的完全二叉树的深度为[log₂n]+1，其中[log₂n]+1是向下取整。满二叉树的深度为k=log₂(n+1);

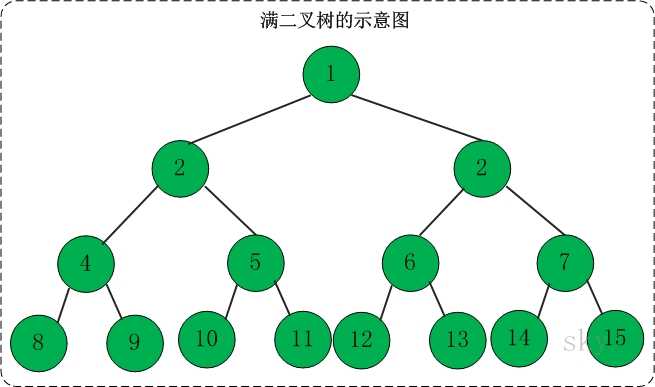
满二叉树：高度为h，由2^h-1个节点构成的二叉树称为满二叉树。

二、二叉树的三种遍历方式

（1）先序遍历：根节点 -> 左子树 ->右子树

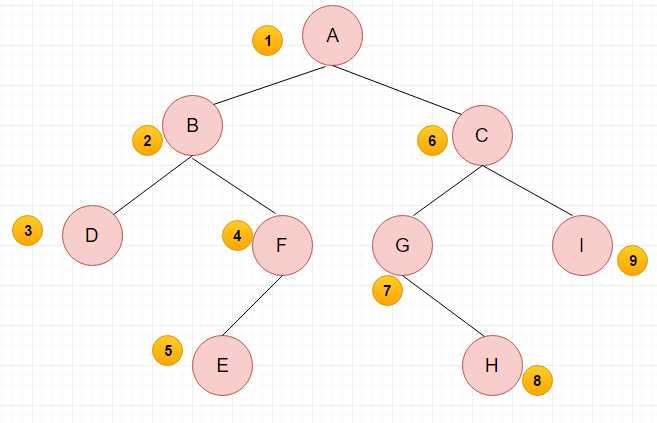
（2）中序遍历：左子树 -> 根节点 -> 右子树

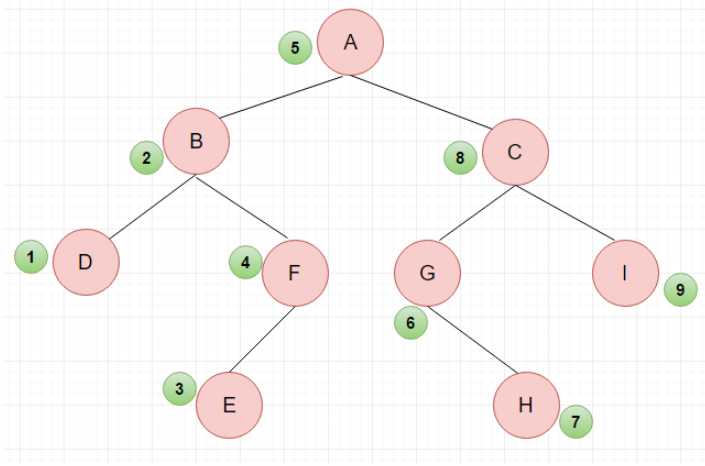
（3）后序遍历：左子树 -> 右子树 -> 根节点

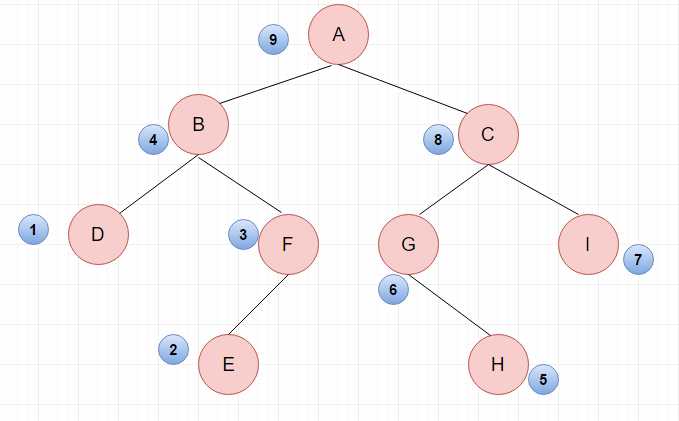
获得遍历顺序的方法原则就是：采用递归的方式遍历

数据结构之二叉树

标签：span   img   n+1   取整   树根   后序   分享   先序   深度   

原文地址：https://www.cnblogs.com/zf-blog/p/9834813.html