标签:strong 博客 inline class 最大团 位置 矩阵 sid 成本
1000 a+b
1001 平面图最小割->对偶图最短路
1002 就是生成树个数,通过基尔霍夫矩阵可以得出递推式 \(f_i=3f_{i-1}-f_{i-2}+2\),然后高精度算一下
1003 令 \(c[i][j]\) 表示从第 \(i\) 天到第 \(j\) 天从 \(1\) 到 \(n\) 不转换路线的最短距离,然后 \(f[i]\) 表示前 \(i\) 天所需要的最小成本,枚举上一次修改路线的位置 \(j\),即 \(f_i=f_j+c[j+1][i]*(i-j)+K\)
1004 根据 \(\text{Burnside}\)引理 我们要求的就是所有置换的不变元素的平均数,注意我们需要添加一个置换 \(1\ 2 \ 3 \dots n\) 才能成为一个置换群,然后每个置换的不变元素数可以先求出循环节,每个循环必须染同一种颜色,然后用一个三维或四维 \(\text{dp}\) 可以求得
1005 由 \(\text{prufer}\)序列 我们知道,一个合法的方案,对应着一个 \(\text{prufer}\)序列 ,其中度数为 \(d\) 的点在序列中出现 \(d-1\) 次,那么已经确定的 \(d\) 出现次数确定,剩下的空位可以随便填入,判断是否可行($\sum ({d_i-1}) \le n-2 $),若可行,答案就为 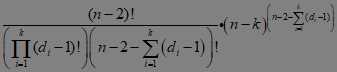
其中 \(k\) 代表 \(d_i\) 不为 \(-1\) 的 \(i\) 的个数
1006 参见cdq的论文 《弦图与区间图》,我们知道答案就是最大团的点数,并且通过按照完美消除序列的反向染色就是最优解,可以用最大势算法求出完美消除序列
1007 单调栈维护上凸壳
1008 用总数 \(m^n\) 减去不符合答案的方案数 \(m*(m-1)^n\)
1009 直接数位\(\text{dp}\),先处理不喜欢的串得到转移方程,我们可以得到复杂度 \(O(400n)\) 的做法,然后用矩阵快速幂优化即可
1010 斜率优化\(\text{dp}\),推荐看 \(\text{hzwer}\)的博客
标签:strong 博客 inline class 最大团 位置 矩阵 sid 成本
原文地址:https://www.cnblogs.com/wawawa8/p/9835875.html