标签:else 其他 png struct prim continue 线性 ring 重要
本文主要介绍了整数快速幂、矩阵快速幂及其应用,以题为例重点展示了使用细节。
我们要计算一个整数x的n次方,即x^n,普通的方法是连乘,这里介绍一种效率非常高的计算幂运算的算法——反复平方法。
首先考虑加速幂运算的方法,如果n=2^k,则可以将x^n = ((x2)2)..,即只要做k次平方运算就可以求得x^n。然后由此我们可以想到,先将n表示为2的幂次之和,即x^n = 2k1 + 2k2 + 2k3... ,那么 x^n = x2^k1 * x2^k2 * x2^k1 ...,只需在求x2^i 的同时进行计算就好了。最终得到O(logn)的计算幂运算的算法。
比如计算x^22 = x^16 * x^4 * x^2,其中22的二进制数是10110,也就是需要反复平方3次。代码如下:
1 typedef long long ll; 2 ll qpow(ll x, ll n) { 3 ll res = 1; 4 while(n) { 5 if(n&1) 6 res = res * x; //如果二进制最低位为1,则乘上x^(2^i) 7 x = x * x; //将x平方 8 n >>= 1; //n/2 9 } 10 return res; 11 }
在实际应用中有时还需要求解x^n%mod。代码如下:
1 typedef long long ll; 2 ll qpow(ll x, ll n, ll mod) { 3 ll res = 1; 4 while(n) { 5 if(n&1) 6 res = res * x % mod; //如果二进制最低位为1,则乘上x^(2^i) 7 x = x * x % mod; //将x平方 8 n >>= 1; //n/2 9 } 10 return res; 11 }
看一道例题:UVA 10006 Carmichael Numbers
判断是否是C数,需要满足以下两个条件
1.不是素数.
2.对任意的1<x<n都有x^n和x同余模n.
代码如下:
1 #include <cstdio> 2 #include <cmath> 3 typedef long long ll; 4 5 ll qpow(ll x, ll n, ll mod) { 6 ll res = 1; 7 while(n) { 8 if(n&1) 9 res = res * x % mod; 10 x = x * x % mod; 11 n >>= 1; 12 } 13 return res; 14 } 15 bool isprime(ll x) { 16 if(x == 0 || x == 1) 17 return 0; 18 ll k = (ll)sqrt(x); 19 for(ll i = 2; i < k; i++) { 20 if(x % i == 0) 21 return 0; 22 } 23 return 1; 24 } 25 int main() 26 { 27 ll n; 28 while(scanf("%lld", &n) == 1 && n != 0) { 29 if(isprime(n)) { 30 printf("%lld is normal.\n", n); 31 continue; 32 } 33 ll i; 34 for(i = 2; i < n; i++) { 35 if(qpow(i, n, n) != i % n) 36 break; 37 } 38 if(i == n) 39 printf("The number %lld is a Carmichael number.\n", n); 40 else 41 printf("%lld is normal.\n", n); 42 } 43 return 0; 44 }
现在要求一个矩阵A的m次幂,也就是A^m,首先应该会两个矩阵的乘法,然后知道A^m的结果一定是一个同型矩阵,最后需要理解上面的整数快速幂。剩下的就是将整数换成矩阵操作。代码如下:
1 const int Matrix_size = 2 2 struct Matrix {//定义矩阵 3 int x[Matrix_size][Matrix_size]; 4 }ans, res; 5 /* 6 定义矩阵乘法,A * B, 它们的都是n阶方阵 7 */ 8 Matrix Mmul(Matrix A, Matrix B, int n) { 9 Matrix tmp; 10 for(int i = 1; i <= n; i++) { 11 for(int j = 1; j <= n; j++) { 12 tmp.x[i][j] = 0; 13 } 14 } 15 16 for(int i = 1 ; i <= n; i++) { 17 for(int j = 1; j <= n; j++) { 18 for(int k = 1; k <= n; k++) { 19 tmp.x[i][j] += A.[i][k] * B[k][j]; 20 } 21 } 22 } 23 return tmp; 24 } 25 /* 26 求res的N次方,n是res的阶数 27 */ 28 void qmpow(int N, int n) { 29 for(int i = 1; i <= n; i++) { 30 for(int j = 1; j <= n; j++) { 31 res.x[i][j] = i == j ? 1 : 0; 32 } 33 } 34 35 while(N) { 36 if(N&1) 37 ans = Mmul(ans, res); 38 res = Mmul(res, res); 39 N >>= 1; 40 } 41 }
利用上面的矩阵快速幂算法可以快速的求解一个矩阵的n次幂,那么求一个矩阵的n次幂有什么用呢?
1.求第n项斐波那契数
根据斐波那契数的定义 F0 = 0,F1 = 1;
Fn = Fn - 1 + Fn - 2(n>=2).
可以用矩阵表示为:
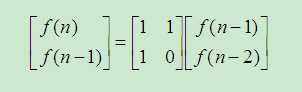
进一步递推得到:
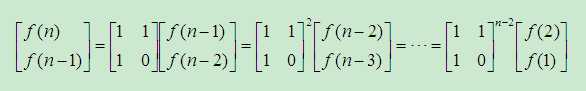
这里需要求的是右边系数矩阵的n-2次幂,然后代入前两项即可求得f(n),也就是第n项斐波那契数。
下面看一道例题:HDU 6198 number number number
题意
先给出了斐波那契数列的定义
F0 = 0, F1 = 1;
Fn = F n - 1 + F n - 2.
再给出坏数的定义,给一个整数k,如果一个整数n不能有k个任意的(可重复)的斐波那契数组成,就成为是一个坏数。现给出k,问最小的坏数是多少,答案对998244353取模。
解题思路
应暴力的方法是不行了,因为给出的k很大。先观察前几项可得:
当k = 1时,4 = 5 - 1 = F(2 * 1 + 3) - 1;
当k = 2时,12 = 13 - 1 = F(2 * 2 + 3) - 1;
问题变成了求解第2 * k + 3项斐波那契数,又因为k很大,就需要使用矩阵快速幂解决了。
根据定义我们定义前两项是1和1,系数矩阵是1,1,1,0,求第n项需要计算系数矩阵的n-2次幂,然后乘上前两项,得到F(n)和F(n - 1)。
代码如下:
1 #include <cstdio> 2 #include <cstring> 3 typedef long long ll; 4 const int mod = 998244353; 5 struct Matrix { 6 ll x[2][2]; 7 }; 8 Matrix Mmul(Matrix a, Matrix b) { 9 Matrix tmp; 10 memset(tmp.x, 0, sizeof(tmp.x)); 11 for(int i = 0; i < 2; i++) { 12 for(int j = 0; j < 2; j++) { 13 for(int k = 0; k < 2; k++) { 14 tmp.x[i][j] = (tmp.x[i][j] + a.x[i][k] * b.x[k][j] % mod) % mod; 15 } 16 } 17 } 18 return tmp; 19 } 20 Matrix Mqpow(Matrix a, ll n) { 21 Matrix tmp; 22 for(int i = 0; i < 2; i++) { 23 for(int j = 0; j < 2; j++) { 24 tmp.x[i][j] = i == j ? 1 : 0; 25 } 26 } 27 28 while(n) { 29 if(n&1) 30 tmp = Mmul(tmp, a); 31 a = Mmul(a, a); 32 n >>= 1; 33 } 34 return tmp; 35 } 36 int main() 37 { 38 ll k; 39 while(scanf("%lld", &k) != EOF) { 40 Matrix st; 41 st.x[0][0] = 1; st.x[0][1] = 1; 42 st.x[1][0] = 1; st.x[1][1] = 0; 43 44 Matrix init; 45 init.x[0][0] = 1; init.x[0][1] = 0; 46 init.x[1][0] = 1; init.x[1][1] = 0; 47 48 st = Mqpow(st, 2 * k + 1); 49 st = Mmul(st, init); 50 printf("%lld\n", (st.x[0][0] - 1 + mod) % mod); 51 } 52 return 0; 53 }
关于矩阵快速幂还有其他一些重要的应用,时间有限,之后再做补充。
关于矩阵快速幂的介绍和应用举例就到这里,主要运用线性代数的知识,做题的时候要找到合适的递推式,然后利用矩阵快速幂优化。
标签:else 其他 png struct prim continue 线性 ring 重要
原文地址:https://www.cnblogs.com/wenzhixin/p/9818747.html