标签:tps cst turn using space 题解 就是 输入格式 cdn
坑题,别人的题解我看了一个下午没一个看得懂的,我还是太弱了。
输入格式:
输入仅有一行,包含两个正整数 q, n,分别表示问题编号以及叶结点的个数。
输出格式:
输出仅有一行,包含一个实数 d,四舍五入精确到小数点后 6 位。如果 q = 1,则 d 表示叶结点平均深度的数学期望值;如果 q = 2,则 d 表示树深度的数学期望值。

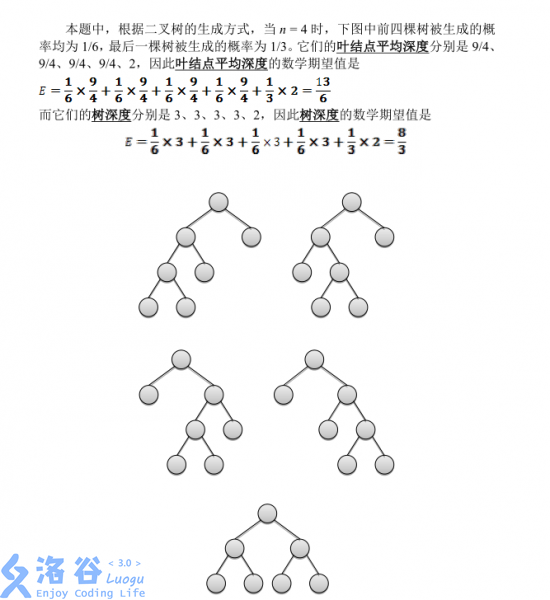
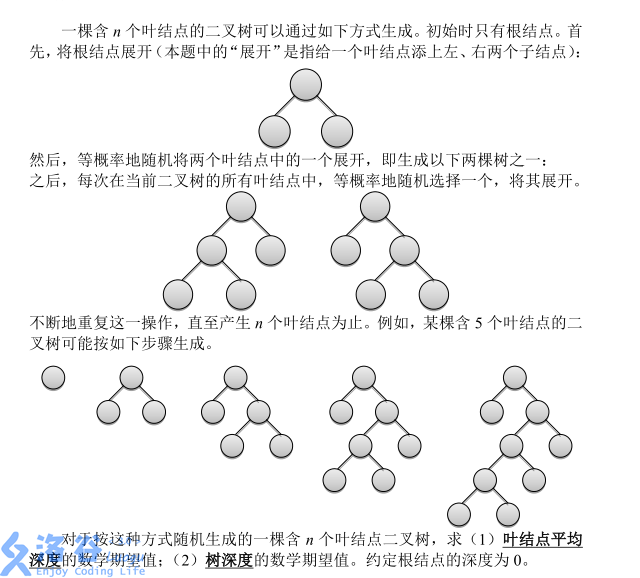
第一问很水,考虑每次新拓展节点就是让树的总深度加上 2
也就是: $$f[i]= \dfrac{f[i-1]*(i-1) + f[i-1] + 2 }{i}$$
意思就是原来 i-1 个节点的平均深度,乘上 (i-1) 变成深度和,然后再加一次 平均深度,然后加 2 ,除以 i 个叶子结点得到当前答案。
化简后式子就变成了: $$f[i]=f[i-1] + \dfrac{2} {i} $$
然后来到第二问(关键问题)。
首先这是概率期望 dp ,于是我们考虑设计状态。
那么我们让 $f[i][j]$ 表示 i 个叶子节点,深度为 j 的概率(是概率)。
那么转移就是: $$ f[i][j] = \dfrac{ f[k][j-1] + f[i-k][j-1]-f[k][j-1] \times f[i-k][j-1] } {i-1} $$
其中 f[i][j] 表示新树状态,f[k][j-1] 为左子树状态,f[i-k][j-1] 为右子树状态。
很多题解到这儿就没了,就没了!也不解释一下的说(尤其 i-1 解释的是真草率)。
最后我自己口胡了一下大概可能也许想通了。
首先 f[i][j] 是我们现在构造出的树的状态,也就是说我们用两个子树拼凑出了一棵新树,而根是新加节点(新加节点会使得左右子树所有叶子结点深度均增加 1 )。
所以这点很重要,也是尤其关键的一步,在强调一遍,f[i][j] 只是代表了新树的形态,且是已经确定了的形态。
那么形成这棵树的概率也就是上面的转移式了,左子树有 j-1 个节点的概率 + 右子树有 j-1 个节点的概率 - 左右子树同时有 j-1 个节点的概率(容斥)。
接着呢? 我们考虑除去 i-1 的意义(自己的想法而已):
我们让当前的这棵树回到上一个状态,也就是说我们令这棵树最后一次叶子结点的扩展取消,回到 i-1 的状态。 (请脑补)
然后聪明的你已经想出来了,这时候要达到当前状态的概率是? 当然是 1/(i-1) 。因为当前这棵树删除的节点扩展回来的概率就是 1/(i-1)。
然后问题就解决了,放代码(非常短啊)。
1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 using namespace std; 5 int q,n; double ans,f[111][111]; 6 int main(){ scanf("%d%d",&q,&n); 7 if(q==1){ 8 for(int i=2;i<=n;++i) ans+=2.0/i; 9 return printf("%.6lf\n",ans),0; 10 } f[1][0]=f[2][1]=f[3][2]=1; 11 for(int i=4;i<=n;++i) for(int j=1;j<=n;++j) 12 for(int k=0;k<j;++k) for(int l=0;l<i-j;++l) 13 f[i][max(k,l)+1]+=(f[j][k]*f[i-j][l])/(i-1); 14 for(int i=1;i<n;++i) ans+=f[n][i]*i; return printf("%.6lf\n",ans),0; 15 }
标签:tps cst turn using space 题解 就是 输入格式 cdn
原文地址:https://www.cnblogs.com/Judge/p/9837561.html