标签:一个 queue sed target match hung div 二分图 center
| Time Limit: 1000MS | Memory Limit: 10000K | |
| http://poj.org/problem?id=1486 |
Description
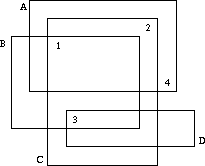
Input
Output
Sample Input
4 6 22 10 20 4 18 6 16 8 20 2 18 10 24 4 8 9 15 19 17 11 7 21 11 2 0 2 0 2 0 2 0 2 1 1 1 1 0
Sample Output
Heap 1 (A,4) (B,1) (C,2) (D,3) Heap 2 none
题解:这题就是烦人的幻灯片的改编版,原来是要求全部匹配,这次是要求输出最大的匹配(我因为这个WA了一下午,我自己都佩服自己);
中间有不确定的不用管;
1.拓扑:于是拓扑排序时就不能只看幻灯片或者数字的度数,要两者结合才能找最大匹配,因为幻灯片一对多或者数字一对多都是存在的;

#include<cstdio> #include<queue> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int M = 70; int xl[M], xr[M], deg[M], yl[M], yr[M], xp[M], mp[M][M], cp[M]; bool vis[M]; int main(){ int idc = 0, n; while(scanf("%d", &n) && n){ memset(deg, 0, sizeof(deg)); memset(mp, 0, sizeof(mp)); memset(cp, 0, sizeof(cp)); memset(vis, 0, sizeof(vis)); int ans = 0; for(int i = 1; i <= n; i++)scanf("%d%d%d%d", &xl[i], &xr[i], &yl[i], &yr[i]); for(int i = 1; i <= n; i++){ int x, y; scanf("%d%d", &x, &y); for(int j = 1; j <= n; j++) if(x <= xr[j] && x >= xl[j] && y <= yr[j] && y >= yl[j]){ mp[i][j + n] = mp[j + n][i] = 1; deg[i]++;deg[j + n]++; } } queue <int> q; for(int i = 1; i <= 2*n; i++) if(deg[i] == 1){ q.push(i); } while(!q.empty()){ int u = q.front(); q.pop(); if(vis[u])continue; vis[u] = 1; for(int i = 1; i <= 2 * n; i++){ if(mp[u][i]){ cp[u] = i, cp[i] = u; vis[i] = 1; deg[i]--; deg[u]--; for(int j = 1; j <= 2*n; j++) if(mp[i][j]) { deg[j]--, mp[i][j] = mp[j][i] = 0; if(deg[j] == 1)q.push(j); } break; } } } for(int i = 1; i <= n; i++) if(cp[i])ans = -1; printf("Heap %d\n", ++idc); if(ans == 0)puts("none"); else { for(int i = 1 + n; i <= 2*n; i++) if(cp[i]){ printf("(%c,%d) ", i - n - 1 + ‘A‘, cp[i]); } puts(""); } puts(""); } }
2.二分图匹配,因为幻灯片和数字是一一对应关系,所以可以往这方面联想;
原图显然是找一个完美匹配,必须这个匹配必须唯一;
我们考虑这个匹配中的边,如果删除他,匹配数减少,说明他是一条必须边,这个匹配是可以唯一确定的;
我们就枚举每条边看是否为必须边

#include<cstdio> #include<queue> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int M = 70; int xl[M], xr[M], yl[M], tot, t[M], yr[M], mp[M][M], lik[M]; bool vis[M]; int cc, n; bool dfs(int u){ for(int i = 1 + n; i <= 2 * n; i++){ if(mp[u][i] && mp[u][i] != cc && !vis[i]){ vis[i] = 1; if(!lik[i] || dfs(lik[i])){ lik[i] = u; lik[u] = i; return 1; } } } return 0; } int hungry(){ memset(lik, 0, sizeof(lik)); int ans = 0; for(int i = 1; i <= n; i++){ memset(vis, 0, sizeof(vis)); if(dfs(i))ans++; } return ans; } int main(){ int idc = 0; while(scanf("%d", &n) && n){ memset(t, 0, sizeof(t)); memset(mp, 0, sizeof(mp)); cc = 0; tot = 0; int ans = 0; for(int i = 1; i <= n; i++)scanf("%d%d%d%d", &xl[i], &xr[i], &yl[i], &yr[i]); for(int i = 1; i <= n; i++){ int x, y; scanf("%d%d", &x, &y); for(int j = 1; j <= n; j++) if(x <= xr[j] && x >= xl[j] && y <= yr[j] && y >= yl[j])mp[j][i + n] = ++tot; } printf("Heap %d\n", ++idc); int Max = hungry(), fg = 0; for(int i = 1; i <= n; i++)t[i] = lik[i]; for(int i = 1; i <= n; i++){ if(t[i]){ cc = mp[i][t[i]]; int tmp = hungry(); if(tmp < n) printf("(%c,%d) ", i - 1 + ‘A‘, t[i] - n), fg = 1; } } if(!fg)printf("none"); puts("");puts(""); } }
标签:一个 queue sed target match hung div 二分图 center
原文地址:https://www.cnblogs.com/EdSheeran/p/9838415.html