标签:先序遍历 sub toc process 两种 树的高度 知识 分类 else
目录
数据结构分类中有一种很常见的结构,那就是树,树的分类很多种,包括二叉树、二叉搜索树、红黑树、B+树等等,但大多数都是基于二叉树的衍生结构,所以今天来学习下二叉树。
定义:二叉树是每个结点最多有两个子树的树结构。通常子树被称作 “左子树”(left subtree)和 “右子树”(right subtree),最顶层的节点叫做 "根" 。
逻辑上,二叉树可以分成五种形态,分别是:
1) 空二叉树
2) 只有一个根节点的二叉树
3)只有跟和左子树
4)只有跟和右子树
5)根和左右子树 (完全二叉树)
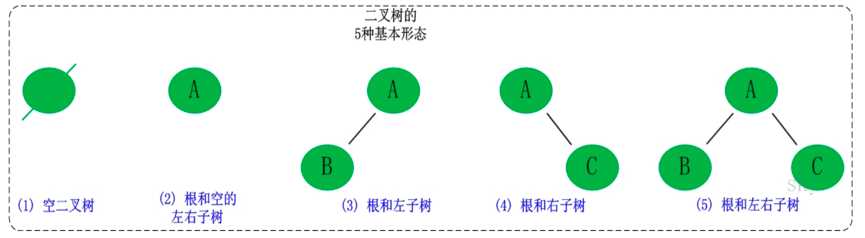
注:二叉树是递归定义的,也就是理论上每个节点都可以无限延伸二叉树的结构,所以每个节点都有左右子树子分,上面的形态只是一种简单的展示。
性质1:二叉树中所有结点的度数均不大于2
性质2:二叉树第i层上的结点数目最多为2i-1(i>=1)
性质3:深度为k的二叉树至多有2k-1个结点(k>=1)
性质4:包含n个结点的二叉树的高度至少为(log2n)+1
性质5:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
性质4的证明:
(1) 基于性质1,我们知道二叉树的节点度数最多不大于2,所以这里假设n0表示度为0的结点个数, n1表示度为1的结点个数,n2表示度为2的结点个数。三类结点加起来为总结点个数,于是便可得到:n=n0+n1+n2
(2) 基于性质1,我们又可以得出,树的总度数为度数0,1,2的度数加上根节点,也就是 n=n0 * 0 + n1 * 1 + n2* 1 + 1
结合上面的(1) 和 (2)的证明就可以得出 n0=n2+1 。
在将二叉树的遍历前,我们需要先实现二叉树,根据二叉树的特点,其包含了节点本身的数据,左子树和右子树,用Java代码可以这样表示
public class Node {
/* * 一个二叉树包括 数据、左右孩子 三部分 */
private int mData;
private Node mLeftChild;
private Node mRightChild;
public Node(int data, Node leftChild, Node rightChild) {
mData = data;
mLeftChild = leftChild;
mRightChild = rightChild;
}
public int getData() {
return mData;
}
public void setData(int data) {
mData = data;
}
public Node getLeftChild() {
return mLeftChild;
}
public void setLeftChild(Node leftChild) {
mLeftChild = leftChild;
}
public Node getRightChild() {
return mRightChild;
}
public void setRightChild(Node rightChild) {
mRightChild = rightChild;
}
}
每一个二叉树的节点都可以用 Node 类表示,下面开始讲述其遍历方式。
前面说了,二叉树是一种递归的结构,每个节点都可以有左右子树的结构,而二叉树的遍历也是个递归遍历的过程,使得每个节点有且只有被访问一次。
按照遍历结构的顺序,一般将二叉树的遍历分为三种:
遍历方式:
代码实现:
public void firstOrder(Node node){
if (node == null){
return;
}
showData(node);
firstOrder(node.getLeftChild());
firstOrder(node.getRightChild());
}
//输出节点数据
public void showData(Node node){
if (node == null){
return;
}
System.out.println(node.getData());
}遍历方式:
代码实现:
public void MediumOrder(Node node){
if (node == null){
return;
}
MediumOrder(node.getLeftChild());
showData(node);
MediumOrder(node.getRightChild());
}遍历方式:
代码实现:
public void LastOrder(Node node){
if (node == null){
return;
}
LastOrder(node.getLeftChild());
LastOrder(node.getRightChild());
showData(node);
}以下面的二叉树为例,三种不同的遍历结果为
先序遍历: 1 2 4 5 7 3 6
中序遍历: 4 2 7 5 1 3 6
后序遍历: 4 7 5 2 6 3 1
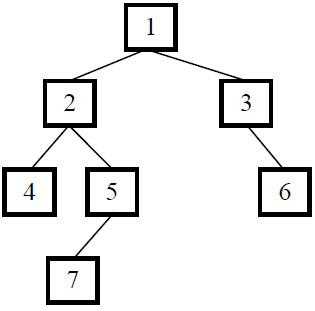
说完二叉树的基本知识后,下面介绍下二叉树的几种延伸结构。
下面介绍两种特殊的二叉树,分别是满二叉树、完全二叉树。
定义:一颗高度为k,拥有2^k-1 个节点。就是说除了叶子节点,每个节点都有左右子树。
示意图如下:
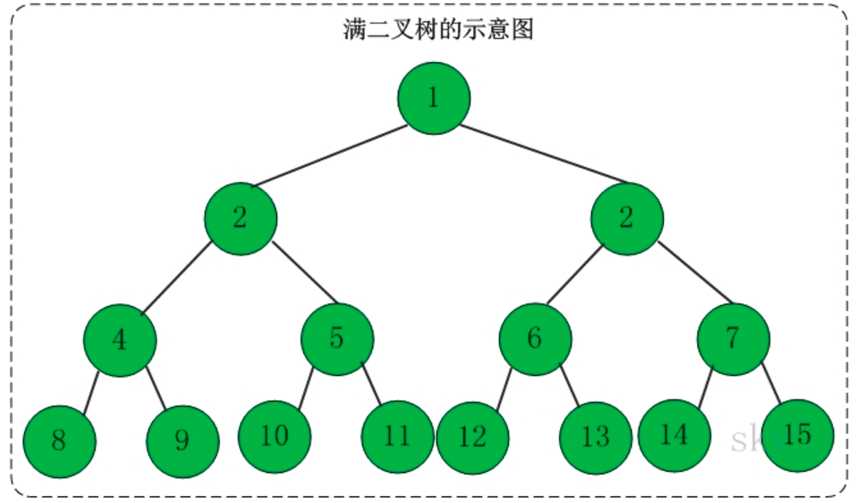
完全二叉树跟满二叉树很类似,但有些许不同,需要满足以下的条件:
给张示意图看下两者的区别:
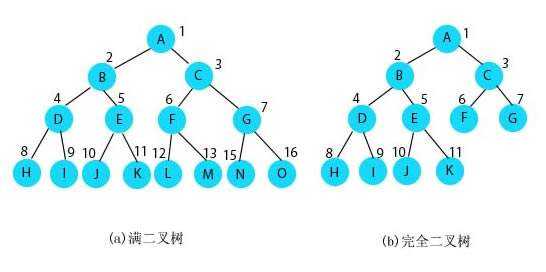
了解两种特殊的二叉树后,我们来做一道算法题巩固一下。
在笔试过程中经常会见到的,就是问你怎么判断一颗二叉树为完全二叉树?
思路:根据完全二叉树的特点,我们知道最后一层的所有节点都在最左边,因此可以按照这样的思路来解题,那就是:在层序遍历的过程中,找到第一个非满节点。满节点指的是同时拥有左右孩子的节点。在找到第一个非满节点之后,剩下的节点不应该有孩子节点;如果有,那么该二叉树就不是完全二叉树。
根据这样的思路,我们可以借助队列,对完全二叉树做广度遍历的方式,下面展示一下代码实现:
public class CompleteTreeChecker {
//辅助空间,队列
private LinkedList<Node> queue = new LinkedList<Node>();
//第n层最右节点的标志
private boolean leftMost = false;
public boolean processChild(Node child) {
if(child != null) {
if(!leftMost) {
queue.addLast(child);
} else {
return false;
}
} else {
leftMost = true;
}
return true;
}
public boolean isCompleteTree(Node root) {
//空树也是完全二叉树
if(root == null) return true;
//首先根节点入队列
queue.addLast(root);
while(!queue.isEmpty()) {
Node node = queue.removeFirst();
//处理左子结点
if(!processChild(node.getLeftChild()))
return false;
//处理右子结点
if(!processChild(node.getRightChild()))
return false;
}
//广度优先遍历完毕,此树是完全二叉树
return true;
}标签:先序遍历 sub toc process 两种 树的高度 知识 分类 else
原文地址:https://www.cnblogs.com/yeya/p/9845880.html