标签：数据结构   archive   log   ade   考试   删除   第四版   方案   技术   

20172330 2018-2019-1 《程序设计与数据结构》第六周学习总结

教材学习内容总结

树

1、树是非线性结构，其元素组织为一个层次结构

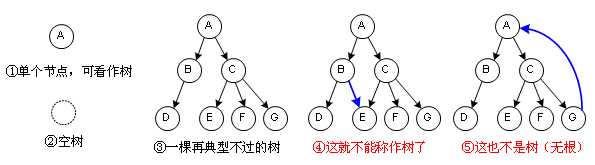
2、树的度表示树中的任意结点的最大子结点数
3、有m个元素的平衡n叉树的高度是lognm
4、树的遍历有4种方法
5、进行层序遍历时可采用队列来储存树中的元素
6、使用数组实现二叉树时，位于位置n的元素的左孩子在(2n+1)的位置，其右孩子在(2*(n+1))的位置
7、树的基于数组的存储链实现方式可以占数组中的连续位置，不管树是不是完全树
8、如何在一般二叉树中添加及删除元素，要取决于树的用途
9、使用决策树可以设计专家系统

二叉树

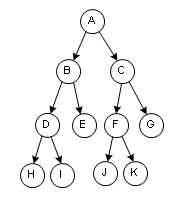
10、二叉查找树时一颗二叉树，对于其中的每个结点，左子树上的元素小于父结点的值，二右子树上的元素大于等于父结点的值
11、如果没有其他的操作，二叉查找树的树形由元素的添加次序来决定
12、最有效地二叉查找树时平衡的，所以每次比较时可以排除一半的元素
13、当从二叉查找树中删除元素时要考虑三种情形，其中的两种比较简单
14、当从二叉查找树中删除有两个子结点的结点时，比较好的办法是用它的中序后继来取代它
15、可以对二叉查找树进行旋转以恢复平衡

部分计算公式

16、二叉树上第i层上的结点数目最多为2^（i-1）(i>=1)
17、深度为k的二叉树至多有2^k-1个结点（i>=1）
18、包含n个结点的二叉树的高度至少为log2（n+1）
19、在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1.

教材学习中的问题和解决过程

• 问题1：树的遍历

• 问题1解决方案：
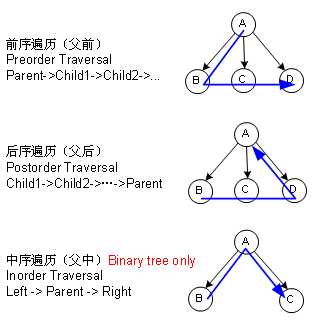
  1、先序遍历——先访问根，再自左向右遍历子树
  2、中序遍历——遍历左子树，然后访问根，然后自左向右遍历余下的各个子树
  3、后续遍历——自左向右遍历各个子树，然后访问根
  4、层序遍历——从树的顶层（根）打包底层，从左至右，访问树中每层的每个结点
  
  例题：
  
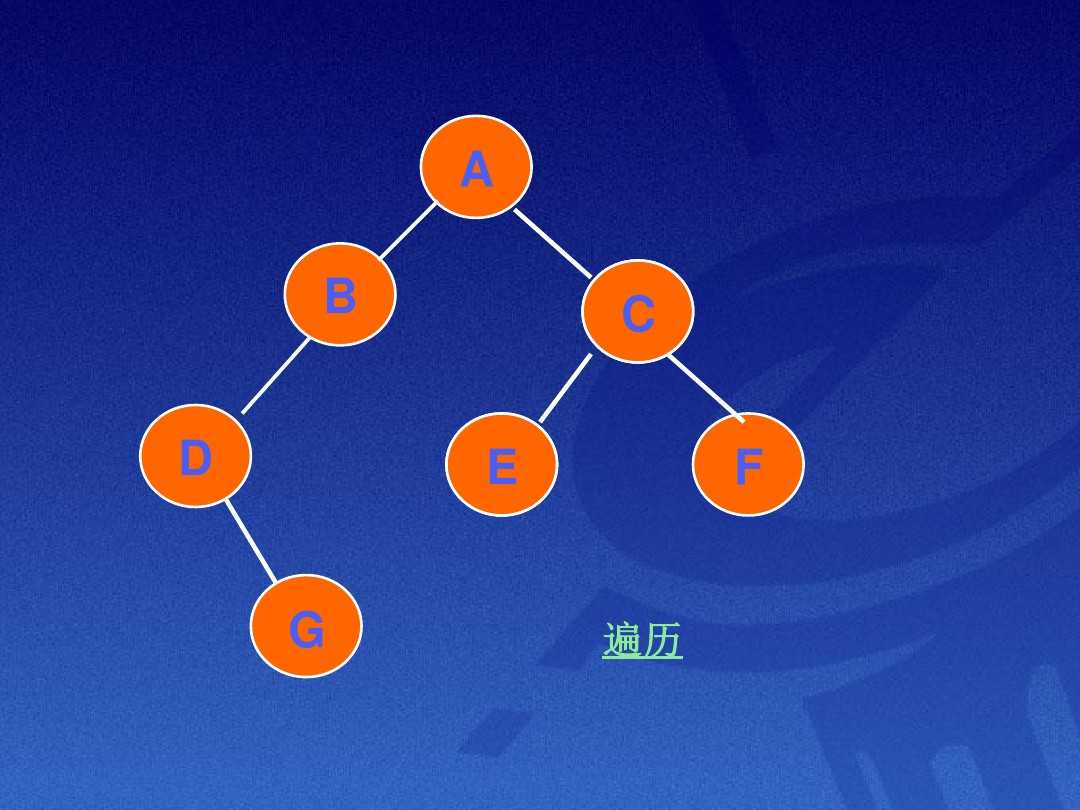
  先序遍历：A B D G C E F
  中序遍历：D G B A E C F
  后续遍历：G D B E F C A

• 问题2：满二叉树和完全二叉树的区别

• 问题2解决方案
  满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
  完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。
  满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

代码调试中的问题和解决过程

• 问题1：在编写树的方法时，RemoveFirst方法一直报错
• 问题1解决方案：在检查后发现是在ListADT时没有写进去导致出现了错误。
  

代码托管

上周考试错题总结

无

结对及互评

• 基于评分标准，我给严域俊的博客打分：7分。得分情况如下：

正确使用Markdown语法（加1分）

模板中的要素齐全（加1分）

教材学习中的问题和解决过程, （加3分）

感想，体会真切的（加1分）

点评认真，能指出博客和代码中的问题的（加1分）

• 博客中值得学习的或问题：
  • 图片和文字相结合，方便理解。
  • 增加了博客中的目录，方便查看，同时样式进行了更新，显得更加美观
  • 阅读了许多资料，使得博客更有说服力。
• 代码中值得学习的或问题：
  - commit依旧很详细，有条理性。

点评过的同学博客和代码

• 本周结对学习情况
  • 20172333
  • 结对学习内容
    教材第9章，运行教材上的代码
    完成课后自测题，并参考答案学习
    完成课后自测题，并参考答案学习
    完成程序设计项目：至少完成PP9.2、PP9.3

其他（感悟、思考等，可选）

这一周花了点心思在这一章上面，也好好阅读了很多内容，掌握的还算可以。

学习进度条

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

• 计划学习时间:10小时

• 实际学习时间:10小时

参考资料

• 《Java程序设计与数据结构教程（第四版）》

• 《Java程序设计与数据结构教程（第四版）》学习指导

20172330 2018-2019-1 《程序设计与数据结构》第六周学习总结

标签：数据结构   archive   log   ade   考试   删除   第四版   方案   技术   

原文地址：https://www.cnblogs.com/linanlalala/p/9844057.html