「一本通 1.2 练习 3」灯泡（三分/公式法）（三角函数，计算几何）

标签：bmp   scanf   最大值   math   输出   return   san   大于   sdn   

传送门

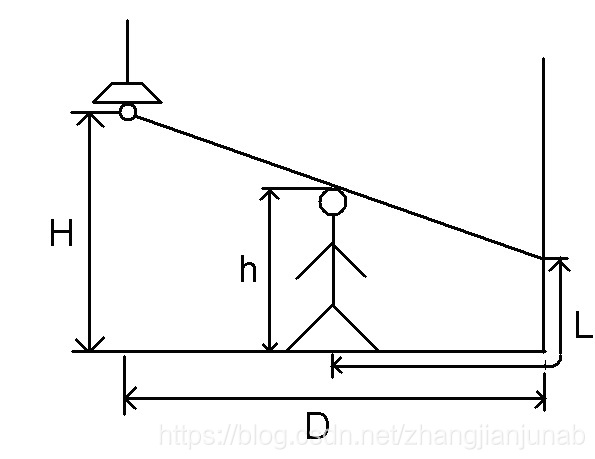
这道题要用带一点点三角函数。。。

不用怕，只要有理性的思维，是可以知道怎么做的

度娘！

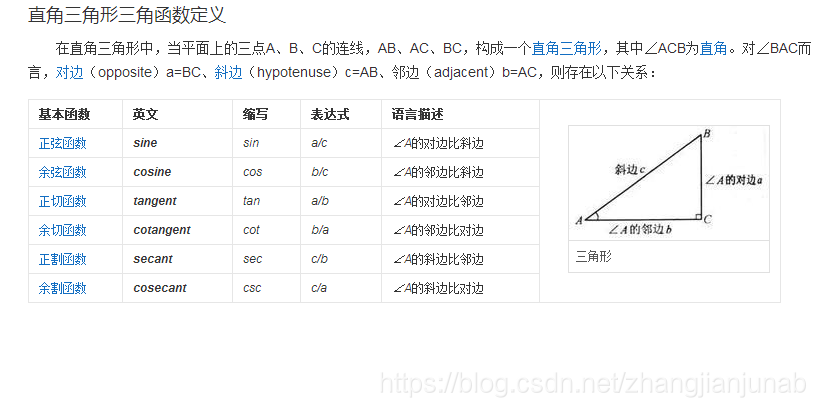
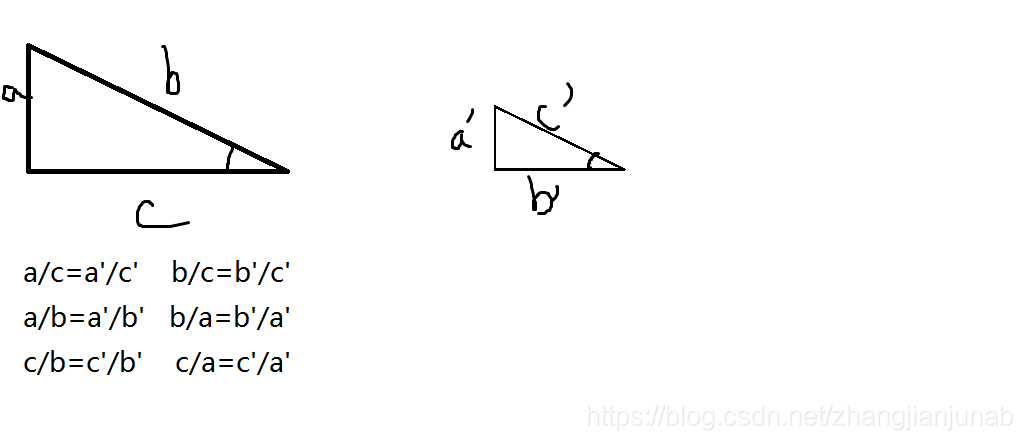
说说我对三角函数的理解吧，简单来说，就是如果你知道直角三角形的一个锐角，那你就知道了这个直角三角型的形状了（求出三个角的角度数），那么如果由另一个直角三角型的三个角也跟这个三角形相等，那么他们两个是可以通过比例转化的，他们三条边中任意两条边之比也相等（也就是任意两条边之比如果角的度数固定了，那么这俩条边的比就固定了）。

安利：

那么，假设人的影子没有在墙上，那么，人从灯底往右走，走越远影子越长！那么最长的情况就是这样：

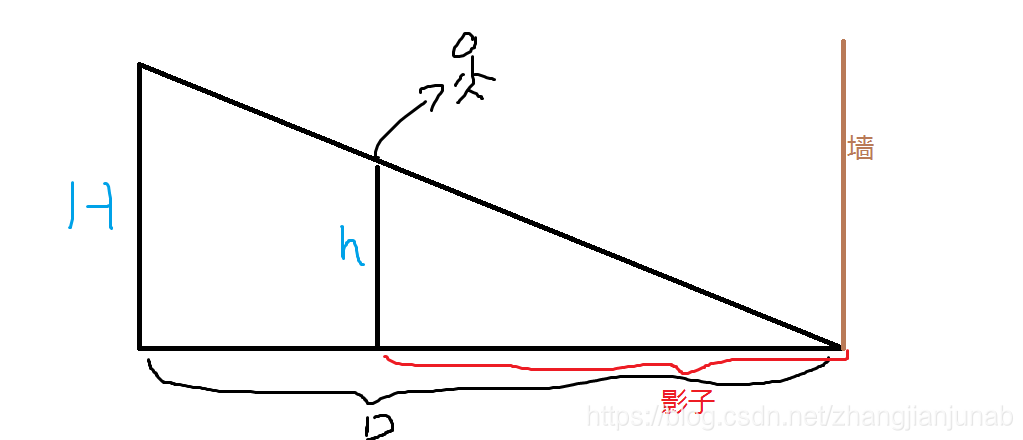
由于比相同，设影长为L，设人离灯x米远。
\[H:D=h:L\]
\[所以Dh=HL\]
\[Dh/H=L\]

那么我们得出了，在影子全在地上，L的最大值为Dh/H，这时x为D-Dh/H，设left=D-Dh/H
那么，如果影子全在墙上，则L=h，x=D，设right为D。
如果影子在墙上，就比较抽象了。。。

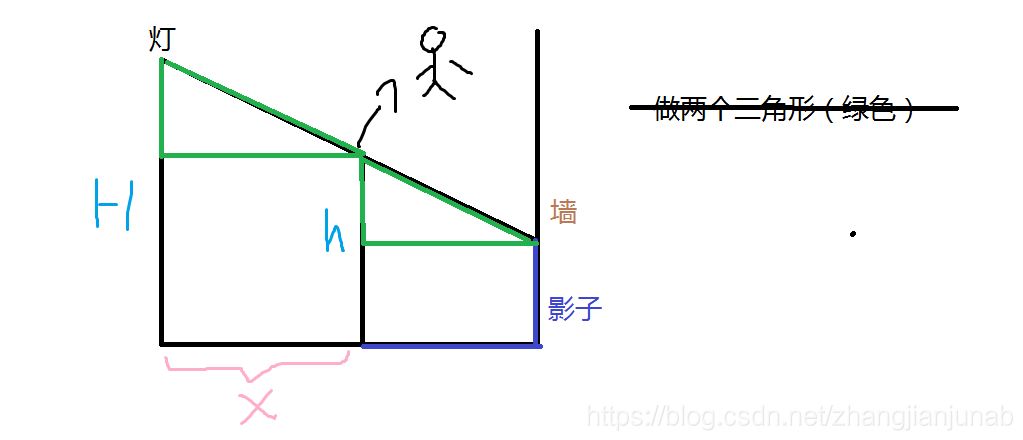
然后呢。。。？

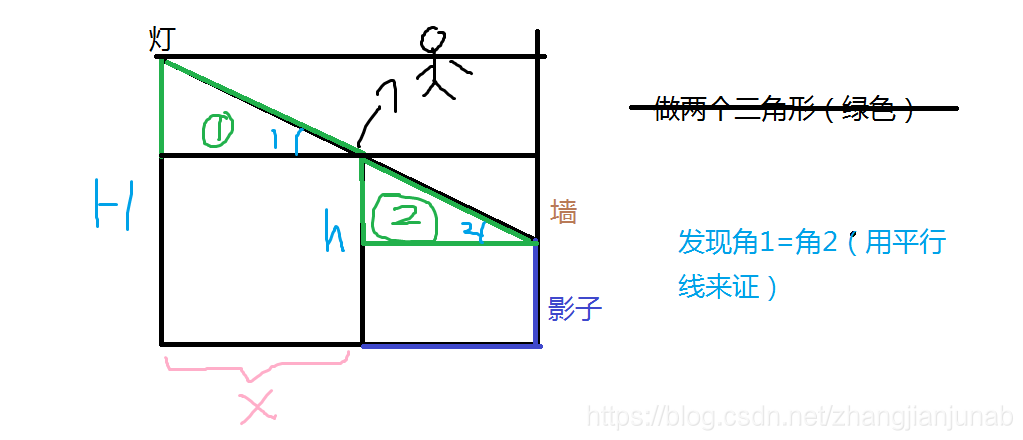
那么:

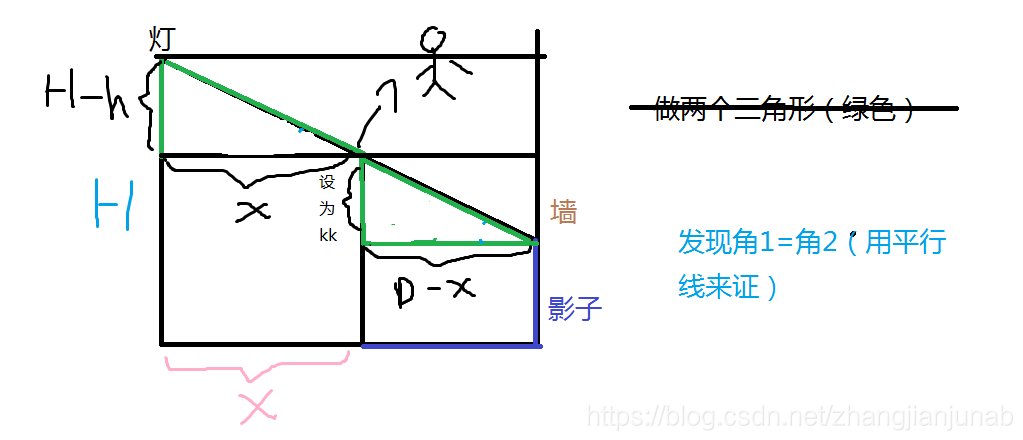
\[那么（H-h）:x=kk:(D-x)\]
\[(H-h)*(D-x)=x*kk\]
\[(H-h)*(D-x)/x=kk\]
那么在墙上的影子就是
\[h-kk=h-(H-h)*(D-x)/x=H-(H-h)*D/x\]
\[L=D-x+(h-kk)=D-x+H-(H-h)*D/x\]
\[=D+H-(x+(H-h)*D/x)\]

那么就是要让\(x+(H-h)*D/x\)取最小值，可以证明，在正数区间，\(x+(H-h)*D/x\)是个开口向上的单峰函数。

证：
情况1：x增加y，\((H-h)*D/x\)减小的数大于y
情况2：x增加y，\((H-h)*D/x\)减小的数小于y
又由于x越大，\((H-h)*D\)/x减小的数字越小，所以，会由情况1慢慢转为情况2，于是便由下降变为上升，成单峰势。

于是，\(D+H-(x+(H-h)*D/x)\)便是个开口向下的单峰函数！（那你整这么一大坨有什么用？）

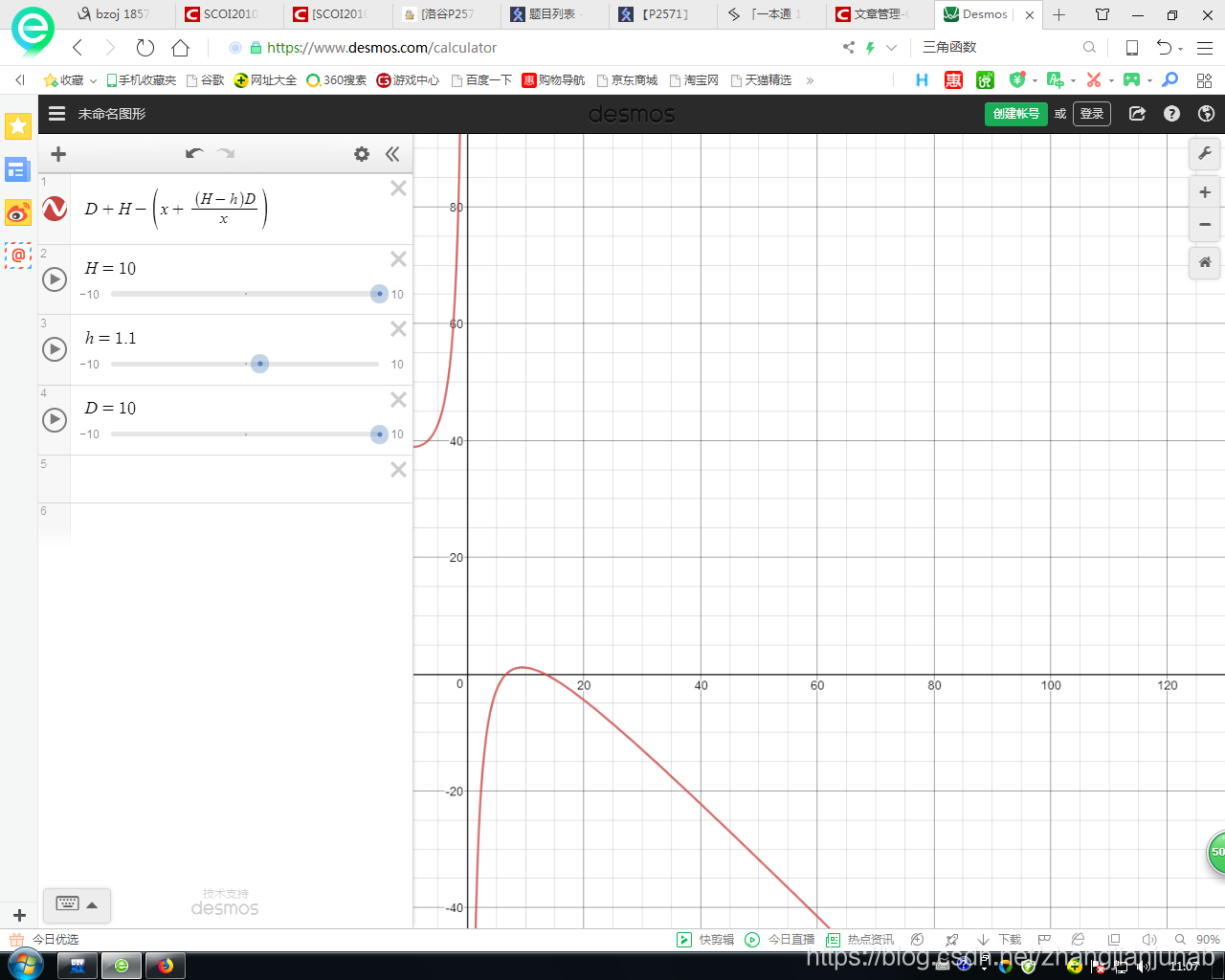
早说有图片！

实现：
l=left,r=right;
当答案=l时，代表影子全在地上的最大值。
当答案=r是时，代表影子全在墙上的最大值。
当答案=(l,r)时，代表影子一半在墙上，一半在地上的最大值。

代码:

#include<cstdio>
#include<cstring>
using  namespace  std;
typedef  long  long  ll;
inline  double  mymax(double  x,double  y){return  x>y?x:y;}
inline  double  cai(double  H,double  h,double  D,ll  x)
{
    double  xx=x/10000.0;
    return  H+D-xx-((H-h)*D)/xx;
}//之前推出的函数 
double  sanfen(double  H,double  h,double  D)
{
    ll  l=ll((D-(h*D)/H)*10000.0),r=ll(D*10000.0);//乘以10000转ll 
    ll  m1,m2;
    while(l<r)//三分 
    {
        m1=(l+r)/2;m2=(l+r)/2+1;
        if(cai(H,h,D,m1)>cai(H,h,D,m2))r=m1;
        else  l=m2;
    }
    return  cai(H,h,D,l);//真象只有一个，l或r就是答案 
}
int  main()
{
    int  T;scanf("%d",&T);
    while(T--)
    {
        double  H,h,D;scanf("%lf%lf%lf",&H,&h,&D);
        printf("%.3lf\n",sanfen(H,h,D));//输出 
    }
    return  0;
}

公式法：

因为这个我看了好久题解（泪奔）(:光速逃

那么，如果是经验丰富的巨佬，一定会想到公式法。。。

\[我们设(H-h)*D为A，设B、C、D为x的一个取值。\]
\[C为x+(H-h)*D/x的单峰\]
\[且B<C<D\]
\[则有B+A/B>C+A/C<D+A/D\]
\[由B+A/B>C+A/C所得\]
\[B-C>A/C-A/B\]
\[B-C>A(B-C)/BC\]
\[BC(B-C)>A(B-C)\]
\[BC<A\]
\[又因为C<B，所以BC<C^2\]
那是不是代表\(A=C^2\)证出来了，耶！想太多

安利：

\[但是，由C+A/C<D+A/D可得\]
\[C-D<A/D-A/C\]
\[C-D<A(C-D)/CD\]
\[CD(C-D)<A(C-D)\]
\[CD>A\]
\[又因为D>C,所以CD>C^2\]
那么我们就可以名正言顺说\(A=C^2\)耶！
所以\(C=sqrt(A)\)
所以，当\(x\)等于\(sqrt((H-h)*D)\)时，\(x+(H-h)*D/x\)位于单峰上，同时\(D+H-(x+(H-h)*D/x)\)也位于单峰上

当然，当\[x<=left\]时，由于\(D+H-(x+(H-h)*D/x)\)是个开口向下的单峰函数，且\(x=[left,right]\)所以x=left。
同理当\(x>=right\)时，x=right！

代码：

#include<cstdio>
#include<cstring>
#include<cmath>
using  namespace  std;
int  main()
{
    int  T;scanf("%d",&T);
    while(T--)
    {
        double  H,h,D;scanf("%lf%lf%lf",&H,&h,&D);
        double  x=sqrt((H-h)*D);
        if(x<=D-(h*D)/H)printf("%.3lf\n",(h*D)/H);//全在地上
        else  if(x>=D)printf("%.3lf\n",h);//全在墙上
        else  printf("%.3lf\n",H+D-x*2);//一部分在地上，一部分在墙上
    }
    return  0;
}

光速逃，耶！写完了！

「一本通 1.2 练习 3」灯泡（三分/公式法）（三角函数，计算几何）

标签：bmp   scanf   最大值   math   输出   return   san   大于   sdn   

原文地址：https://www.cnblogs.com/zhangjianjunab/p/9855482.html