标签：思路   class   ons   代码   tin   颜色不同   for   接下来   getch   

题目背景

“サーヴァント、キャスター、Medea。”--紫魔法师

题目描述

给出一棵仙人掌(每条边最多被包含于一个环，无自环，无重边，保证连通)，要求用最少的颜色对其顶点染色，满足每条边两个端点的颜色不同，输出最小颜色数即可

输入描述

第一行包括两个整数n,m，表示顶点数和边数
n <= 100000, m <= 200000
接下来m行每行两个整数u,v，表示u,v之间有一条无向边，保证数据合法

输出描述

一行一个整数表示最小颜色数。

思路：

最开始拿到这题，我是完全懵逼的。无向图求最小染色数，这不是NP问题吗，拿出来考？emmm。。。。。。
经过大佬Czt的点拨，我注意到了题目中的一句话。划重点了，划重点了啊： 给出一颗仙人掌（每条边最多包含于一个环，无自环，无重边，保证联通） 。
也就是说，情况无非就以下几种：


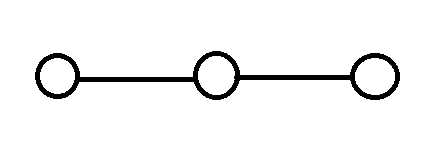
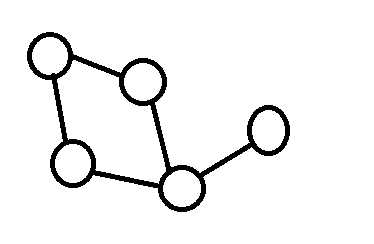
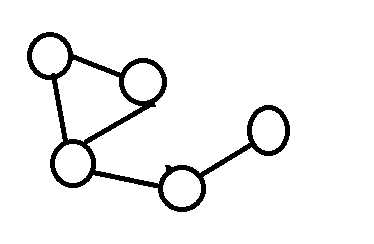
一个点的情况很明显，输出1即可。而一条链无论有多长，都只会用到2种颜色。如果没有奇环的话，也只会用到2种颜色。而有奇环的话则会用到3种颜色。
请读者自己证明，在一个图是仙人掌的情况下，不会有超过3种颜色的图。
所以这道题就只需要搜一下这个图有没有奇环即可。

代码

#include<bits/stdc++.h>
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘) f=0;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘){x=(x<<1)+(x<<3)+(ch&15);ch=getchar();}
  if(f) return x;else return -x;
}
const int N=1e5+10,M=2e5+10;
int n,m,head[N],p,maxn,num[N],flag;
struct data{
    int to,last;
}e[M*2];
bool use[N];
void add(int a,int b){e[++p]=(data){b,head[a]};head[a]=p;}
void dfs(int u){
    use[u]=1;
    for(int i=head[u];i;i=e[i].last){
        int v=e[i].to;
        if(use[v]){
            if((num[u]-num[v]+1)&1) flag=1;
            continue;
        }
        num[v]=num[u]+1;dfs(v);
    }
    return;
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=m;i++){
        int a=read(),b=read();
        add(a,b);add(b,a);
    }
    num[1]=1;
    dfs(1);
    if(n==1) printf("1\n");
    else if(n==2) printf("3\n");
    else printf("%d\n",flag+2);
    return 0;
}

紫魔法师

标签：思路   class   ons   代码   tin   颜色不同   for   接下来   getch   

原文地址：https://www.cnblogs.com/Princeoftheking/p/9860876.html