标签:tor idt 包含 通过 targe problem typedef type 条件
原文链接https://www.cnblogs.com/zhouzhendong/p/CF781E.html
有一个矩形,宽为 w ,高为 h 。一开始会有 w 个球分别从高处的每一个位置开始下落。
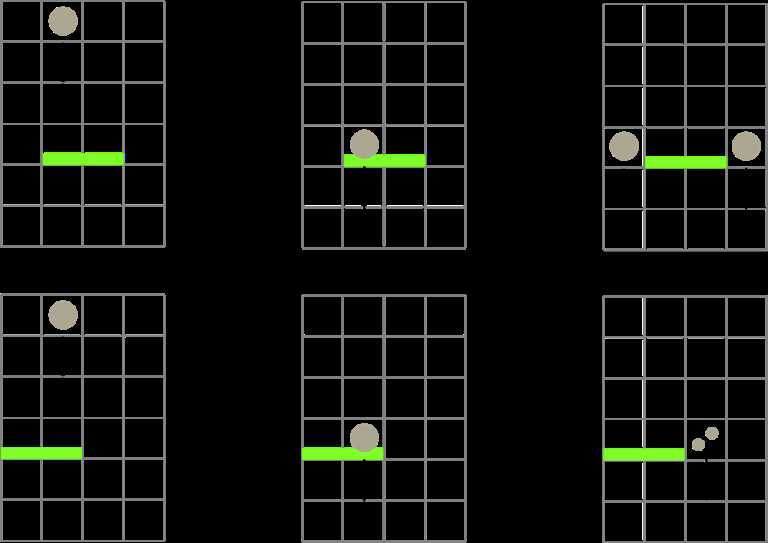
有 n 个挡板,每一个挡板有 4 个属性,分别是 u,L,R,s ,表示当前挡板的高度为 u ,横向覆盖的区间为 L,R ,如果球从高度大于 u+s 的地方开始下落到当前挡板,那么球会穿透当前挡板,否则球会分裂成两个,分别从该挡板的两边从新开始下落(如图的第一行),特殊地,当挡板的一段在边界上时,分裂得到的两个球都会从另一端下降(如图的第二行)。
问最终地面上能收到多少个球。
$w,n\leq 10^5,\ \ \ u,s,h\leq 10^9,\ \ 1\leq L\leq R\leq n$,保证每一行最多只有一个挡板,且不会有挡板两端都到达了边界。
首先,我们观察到如果直接 dp ,转移数就等于 挡板数×2+w (每一个挡板的两侧以及一开始投放的 w 个球)。
关键在于如何找到一个球从每一个位置开始下落会在哪里分裂。
我们来理一理思路:
我们要找的挡板要满足以下条件:
1. 高度小于当前高度。
2. u+s 要大于等于当前高度。
3. [L,R] 要包含当前横坐标。
4. 在满足上述条件的情况下,使得 u 最大。
显然可以发现可以树套树套树。但是这样显然不足以通过此题。
然后我们发现只需要把挡板按照高度从低到高排序,然后依次操作就好了,这样只需要树套树。但是这样的空间复杂度仍然是凉凉的。
于是,接下来是最重要的一步了!
一个挡板的纵向影响区间是 [u,u+s] ,对于这一维,我们可以直接用单调栈维护。
于是我们得到一个 线段树 + 单调栈的做法。可以通过本题。
时间复杂度 $O(n\log n)$ 。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL read(){
LL x=0,f=1;
char ch=getchar();
while (!isdigit(ch)&&ch!=‘-‘)
ch=getchar();
if (ch==‘-‘)
f=-1,ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x*f;
}
const int N=100005,mod=1e9+7;
int n,h,w;
struct Node{
int L,R,h,m,ans;
}a[N];
bool cmph(Node a,Node b){
return a.h<b.h;
}
vector <int> s[N<<2];
void build(int rt,int L,int R){
s[rt].push_back(1);
if (L==R)
return;
int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
build(ls,L,mid);
build(rs,mid+1,R);
}
void Push(vector <int> &s,int x){
while (a[s.back()].m<a[x].m)
s.pop_back();
s.push_back(x);
}
void update(int rt,int L,int R,int xL,int xR,int d){
if (L>xR||R<xL)
return;
if (xL<=L&&R<=xR){
Push(s[rt],d);
return;
}
int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
update(ls,L,mid,xL,xR,d);
update(rs,mid+1,R,xL,xR,d);
}
int query(vector <int> &s,int h){
while (a[s.back()].m<h)
s.pop_back();
return s.back();
}
int query(int rt,int L,int R,int x,int d){
int ans=query(s[rt],d);
if (L==R)
return ans;
int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
if (x<=mid)
return max(ans,query(ls,L,mid,x,d));
else
return max(ans,query(rs,mid+1,R,x,d));
}
int main(){
h=read(),w=read(),n=read();
for (int i=1;i<=n;i++){
a[i].h=read(),a[i].L=read(),a[i].R=read();
a[i].m=min(a[i].h+read(),(LL)h+1);
}
n++;
a[n].h=0,a[n].L=1,a[n].R=w,a[n].m=1.05e9;
sort(a+1,a+n+1,cmph);
a[1].ans=1;
for (int i=0;i<(N<<2);i++)
s[i].clear();
build(1,1,w);
for (int i=2;i<=n;i++){
if (a[i].L==1)
a[i].ans=2*a[query(1,1,w,a[i].R+1,a[i].h)].ans%mod;
else if (a[i].R==w)
a[i].ans=2*a[query(1,1,w,a[i].L-1,a[i].h)].ans%mod;
else
a[i].ans=(a[query(1,1,w,a[i].L-1,a[i].h)].ans
+a[query(1,1,w,a[i].R+1,a[i].h)].ans)%mod;
update(1,1,w,a[i].L,a[i].R,i);
}
int ans=0;
for (int i=1;i<=w;i++)
ans=(ans+a[query(1,1,w,i,h+1)].ans)%mod;
printf("%d",ans);
return 0;
}
Codeforces 781E Andryusha and Nervous Barriers 线段树 单调栈
标签:tor idt 包含 通过 targe problem typedef type 条件
原文地址:https://www.cnblogs.com/zhouzhendong/p/CF781E.html