标签:html sel off extract 概率分布 com 步骤 dip 语料库
主题模型
主题模型理理论
直观版
标准版
公式版
实战
一眼看穿『希拉?里里邮件门』
什么是主体模型?
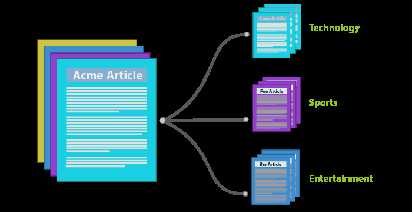
理论解释
理理解整个过程,涉及到?比较复杂数学推导。
一般来说,从公式1?一直推导到公式100,
大部分同学会在公式10左右的时候,就关了了直播,洗洗睡了了
所以,我今天?用3个不不同版本的讲解,从简单到复杂,
来让?大家?一步步理理解主体模型。
据我推测,?大部分?人是可以撑过前两个版本的。
这样,就算第三个版本太过枯燥,你也可以安?心的洗洗睡,?无妨。
么么
直观版
假设某企业想要招聘?一个?工程师,
他们收到了了?一把的简历,
他们想直接通过简历来看谁是?大?牛,谁是彩笔
简历里里通常会包含这些个人特征:

这三个要素,构成了了这家企业的?人?力力总监判断的基础:
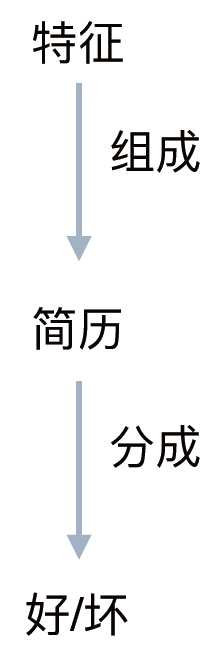
这位人力总监要做的事是:
拿出一份简历
记录下每份简历包含的特征
然而,他并不不知道,这一切代表着什什么
于是他开始猜
拿起一份简历A,
他看到里面说A参加过七?月课程
他就猜这位童鞋的?水平应该很高,八成应该是个好工程师
但是他又看到A的学历只是小学毕业,心里又有了了两成的担忧
他又看到B
又看到C
等等。。。
当然,这个猜,只是猜,没有任何证据可以证实。
但是这位人力总监是久经职场的老司机,他通过经验统计来调整自己的猜想:
- 选一份『张三』的简历,选一个特征『条纹衬衫』
- 为什什么『张三』有可能喜欢穿『条纹衬衫』?也许是因为穿条纹衬衫是优秀
程序员的信仰
- 也就是说,越多的优秀程序员穿『条纹衬衫』,越让人力总监猜想『张三』
的其他个特征也符合优秀程序员的喜好,并且『张三』本人穿『条纹衬衫』
是一个优秀的程序员自我修养的体现
- 继续猜,继续拿『张三』和『条纹衬衫』两个元素。人力总监转念一想,也
有可能爱穿条纹的都是彩笔。
- 于是他按照上面的逻辑,再看看『张三』穿『条纹衬衫』是『彩笔』的可能
性有多少
- 把所有的简历和所有的特征都做个组合,都来猜一下是彩笔还是大牛
久经沙场之后,老司机人力总监掌握了了如下信息:
对于是不是优秀程序员的分类,它通过人头统计大概有了了数
这让他在以后看到新简历的时候,一眼就知道他是不是个优秀程序员
对于每个特征C,他也能说出大概百分之多少的人拥有特征C可以说明他们是优秀的程序员。
总结成公式就是:

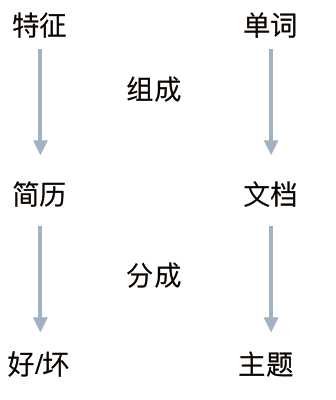
以上,就是我们用现实的例子模拟的LDA模型来区分简历好坏在文本的主题分类中,我们的例子和实际之间的联系如下:
什么是LDA?
Latent Dirichlet Allocation:
是一种无监督的贝叶斯模型
是一种主题模型,它可以将文档集中每篇文档的主题按照概率分布的形式给出。同时它是一种无监督学习算法,在训练时不需要手工标注的训练集,需要的仅仅是文档集以及指定主题的数量量k即可。此外LDA的另一个优点则是,对于每一个主题均可找出一些词语来描述它。
是一种典型的词袋模型,即它认为一篇文档是由一组词构成的一个集合,词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
— wikipedia
什么是贝叶斯模型?
理论
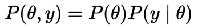
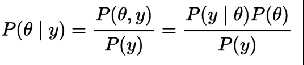
模型
- 用概率作为『可信度』
- 每次看到新数据,就更更新『可信度』
- 需要一个模型来解释数据的生成
先验,后验与似然
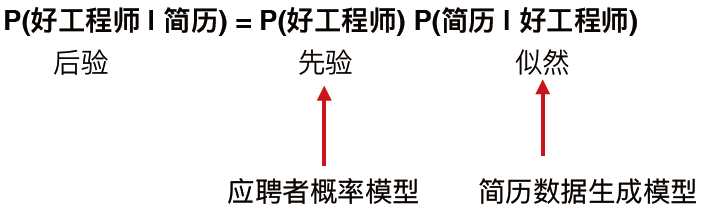
标准版
我们用LDA找寻的就是之前例子里总监大人统计出来的经验:
一份简历的每个特征都是因为本人有一定概率是好/坏程序员,并从好/坏这个分类中以一定概率选择某些特征而组成的
一篇文章的每个词都是以一定概率选择了某个主题,并从这个主题中以一定概率选择某个词语而组成的
P(单词 | 文档) = P(单词 | 主题) * P(主题 | 文档)
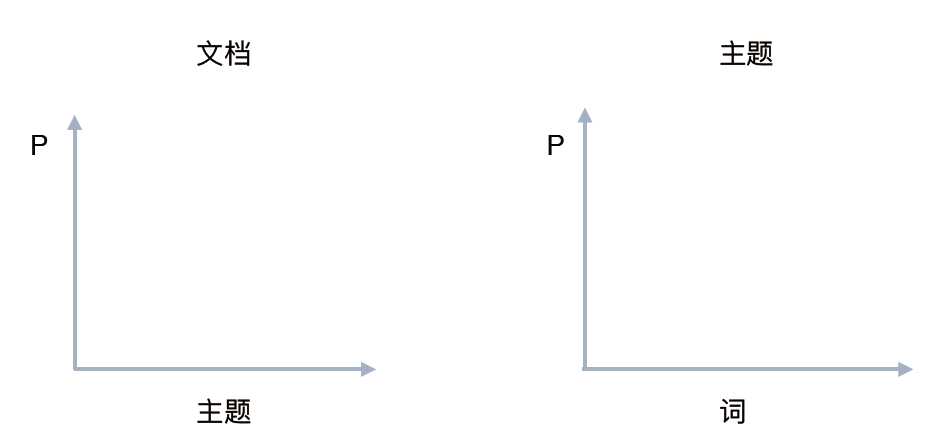
LDA生成过程
对于语料料库中的每篇文档,LDA定义了如下生成过程(generative process):
1.对每一篇文档,从主题分布中抽取一个主题;
2.从上述被抽到的主题所对应的单词分布中抽取一个单词;
3.重复上述过程直至遍历文档中的每一个单词。
稍微具体点儿讲:
(w代表单词;d代表?文档;t代表主题;?大写代表总集合,?小写代表个体。)
标准版
D中每个文档d看作?一个单词序列列<w1,w2,...,wn>,wi表示第i个单词。
D中涉及的所有不同单词组成一个词汇表大集合V (vocabulary),LDA以文档集合D
作为输入,希望训练出的两个结果向量量(假设形成k个topic,V中?一共m个词):
对每个D中的文档d,对应到不不同Topic的概率θd<pt1,...,ptk>,其中,pti表示d对应T中第i个topic的概率。计算方法是直观的,pti=nti/n,其中nti表示d中对应第i个topic的词的数目,n是d中所有词的总数。
对每个T中的topict,生成不不同单词的概率φt<pw1,...,pwm>,其中,pwi表示t生成V中第i个单词的概率。计算方法同样很直观,pwi=Nwi/N,其中Nwi表示对应到topict的V中第i个单词的数目,N表示所有对应到topict的单词总数。
用人话说:
pti=某个词在某个主题中的数目/某个词在某个文档中的数目
pwi=某个词在某个主题中的数量/某个词在所有文档中的数量
所以,LDA的核心公式如下:
P(w|d)=P(w|t)*P(t|d)
直观的看这个公式,就是以Topic作为中间层,可以通过当前的θd和φt给出了文档d中出现单词w的概率。其中p(t|d)利用θd计算得到,p(w|t)利用φt计算得到。
实际上,利用当前的θd和φt,我们可以为一个文档中的一个单词计算它对应任意一个Topic时的p(w|d),然后根据这些结果来更新这个词应该对应的topic。然后,如果这个更新改变了了这个单词所对应的Topic,就会反过来影响θd和φt
LDA学习过程
LDA算法开始时,先随机地给θd和φt赋值(对所有的d和t)。然后:
1.针对一个特定的文档ds中的第i单词wi,如果令该单词对应的topic为tj,可以把上述公式改写为:Pj(wi | ds)=P(wi | tj)*P(tj | ds) = φt*θd
2.现在我们可以举T中的topic,得到所有的pj(wi | ds)。然后可以根据这些概率值结果为ds中的第i个单词wi选择一个topic。最简单的想法是取令pj(wi | ds)最大的tj(注意,这个式子里只有j是变量量)
3.然后,如果ds中的第i个单词wi在这里选择了一个与原先不同的topic(也就是说,这个时候i在遍历ds中所有的单词,而tj理当不变),就会对θd和φt有影响了了。它们的影响又会反过来影响对上面提到的p(w | d)的计算。对D中所有的d中的所有w进行一次p(w | d)的计算并重新选择topic看作一次迭代。这样进行n次循环迭代之后,就会收敛到LDA所需要的结果了。
用人话说:
P(单词|文档)=P(单词|主题)*P(主题|文档)
最终要求的是:P(主题|文档)
已知的是:P(单词|文档)
1,一个文档中,某个词对应一个主题。
2,选择所有主题中的每一个主题进行计算,得到所有的P(单词|文档),然后根据这个概率,为这个词选择一个主题。
3,第二步为这个词选择的主题,不是原先的主题,那么就更新P(单词|主题),P(主题|文档),更新他两的同时也会根据公式得到新的P(单词|文档),知道更新的P(单词|文档)与已知的P(单词|文档)相同,那么P(单词|主题)和P(主题|文档)就可以确定下来
要求的不就是P(主题|文档)么。
搞不懂这些培训机构为什么不说人话!!!
公式版:
现在,我们对LDA的玩法基本了了解了了,
我们终于可以安静的刷刷公式了了(注:尿点时刻):
这一部分的解释,可以参照七月在线创始人July的CSDN博客:
http://blog.csdn.net/v_july_v/article/details/41209515
正经的理理解LDA,分为下述5个步骤:
一个函数:gamma函数
四个分布:二项分布、多项分布、beta分布、Dirichlet分布
一个概念和一个理理念:共轭先验和贝叶斯框架
两个模型:pLSA、LDA
一个采样:Gibbs采样
共轭分布与共轭先验:
![]()
Gamma函数
阶乘函数在实数上的推广。
我们知道,对于整数?而言:
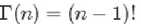
对于实数:
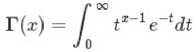
二项分布(Binomial distribution)
二项分布是从伯努利利分布推进的。伯努利利分布,又称两点分布或0-1分布,是一个离散型的随机分布,其中的随机变量量只有两类取值,非正即负{+,-}。而二项分布即重复n次的伯努利利试验,记为 。简言之,只做一次实验,是伯努利利分布,重复做了了n次,是二项分布。二项分布的概率密度
函数为:
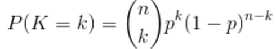
多项分布,是二项分布扩展到多维的情况
多项分布是指单次试验中的随机变量量的取值不不再是0-1的,而是有多种离散值可能(1,2,3...,k)。比如投掷6个?面的骰子实验,N次实验结果服从K=6的多项分布。当然啦,他们加起来的P应该是等于1的。
多项分布的概率密度函数为:
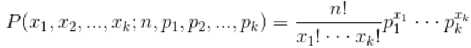
Beta分布,二项分布的共轭先验分布
给定参数a>0和b>0,取值范围为[0,1]的随机变量量 x 的概率密度函数:
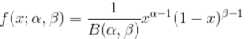
其中:
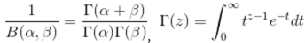
Dirichlet分布,是beta分布在高维度上的推?广

其中
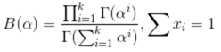
贝叶斯派的思考方式:

几个主题模型(循序渐进):
Unigram model
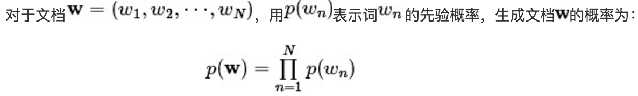
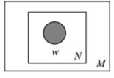
Mixture of unigrams model
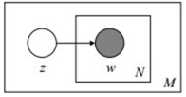
该模型的生成过程是:给某个文档先选择一个主题z,再根据该主题生成文档,该文档中的所有词都来自一个主题。假设主题有z1,z2,z3,...zk,生成文档的概率为:
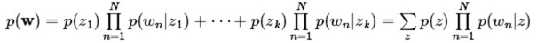
PLSA模型
刚刚的mix unigram模型里里面,一篇文章只给了了一个主题。但是现实生活中,一篇文章可能有多个主题,只不不过是『出现的?几率』不一样。
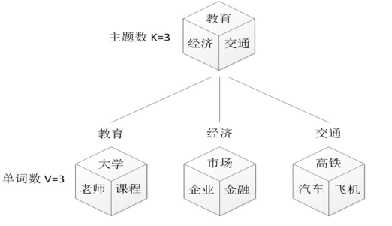
我们定义:

我们的文本生成模型就是:
(还记得什什么是文本生成模型嘛?返回标准版part回顾一下)
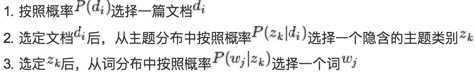
我们通过观测,得到了『知道主题是什么,我就用什么单词』的文本生成模型,那么,根据贝叶斯定律律,我们就可以反过来推出『看见用了了什么单词,我就知道主题是什么』
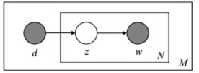

LDA模型
LDA就是在pLSA的基础上加层?贝叶斯框架,即LDA就是pLSA的?贝叶斯版本
PLSA与LDA对比
PLSA

LDA

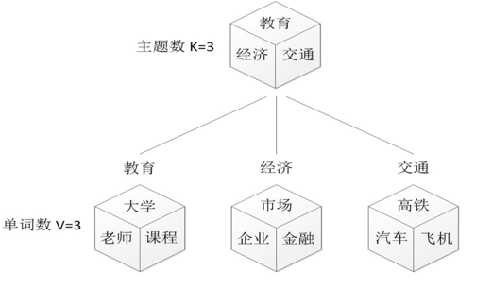
pLSA跟LDA的本质区别就在于它们去估计未知参数所采用的思想不不同,前者?用的是频率派思想,后者用的是贝叶斯派思想。
我们拿到希拉里泄露的邮件,跑一把LDA,看看她平时都在聊什么。
首先,导入我们需要的一些库
import numpy as np import pandas as pd import re
然后,把希婆的邮件读取进来。
这里我们用pandas。不熟悉pandas的朋友,可以用python标准库csv
df = pd.read_csv("../input/HillaryEmails.csv")
# 原邮件数据中有很多Nan的值,直接扔了。
df = df[[‘Id‘,‘ExtractedBodyText‘]].dropna()
上过我其他NLP课程的同学都知道,文本预处理这个东西,对NLP是很重要的。
我们这里,针对邮件内容,写一组正则表达式:
(不熟悉正则表达式的同学,直接百度关键词,可以看到一大张Regex规则表)
def clean_email_text(text):
text = text.replace(‘\n‘," ") #新行,我们是不需要的
text = re.sub(r"-", " ", text) #把 "-" 的两个单词,分开。(比如:july-edu ==> july edu)
text = re.sub(r"\d+/\d+/\d+", "", text) #日期,对主体模型没什么意义
text = re.sub(r"[0-2]?[0-9]:[0-6][0-9]", "", text) #时间,没意义
text = re.sub(r"[\w]+@[\.\w]+", "", text) #邮件地址,没意义
text = re.sub(r"/[a-zA-Z]*[:\//\]*[A-Za-z0-9\-_]+\.+[A-Za-z0-9\.\/%&=\?\-_]+/i", "", text) #网址,没意义
pure_text = ‘‘
# 以防还有其他特殊字符(数字)等等,我们直接把他们loop一遍,过滤掉
for letter in text:
# 只留下字母和空格
if letter.isalpha() or letter==‘ ‘:
pure_text += letter
# 再把那些去除特殊字符后落单的单词,直接排除。
# 我们就只剩下有意义的单词了。
text = ‘ ‘.join(word for word in pure_text.split() if len(word)>1)
return text
好的,现在我们新建一个colum,并把我们的方法跑一遍:
docs = df[‘ExtractedBodyText‘] docs = docs.apply(lambda s: clean_email_text(s))
好,来看看长相:
docs.head(1).values
array([ ‘Thursday March PM Latest How Syria is aiding Qaddafi and more Sid hrc memo syria aiding libya docx hrc memo syria aiding libya docx March For Hillary‘], dtype=object)
我们直接把所有的邮件内容拿出来。
doclist = docs.values
好,我们用Gensim来做一次模型构建
首先,我们得把我们刚刚整出来的一大波文本数据
[[一条邮件字符串],[另一条邮件字符串], ...]转化成Gensim认可的语料库形式:
[[一,条,邮件,在,这里],[第,二,条,邮件,在,这里],[今天,天气,肿么,样],...]引入库:
from gensim import corpora, models, similarities import gensim
为了免去讲解安装NLTK等等的麻烦,我这里直接手写一下停止词列表:
这些词在不同语境中指代意义完全不同,但是在不同主题中的出现概率是几乎一致的。所以要去除,否则对模型的准确性有影响
stoplist = [‘very‘, ‘ourselves‘, ‘am‘, ‘doesn‘, ‘through‘, ‘me‘, ‘against‘, ‘up‘, ‘just‘, ‘her‘, ‘ours‘,
‘couldn‘, ‘because‘, ‘is‘, ‘isn‘, ‘it‘, ‘only‘, ‘in‘, ‘such‘, ‘too‘, ‘mustn‘, ‘under‘, ‘their‘,
‘if‘, ‘to‘, ‘my‘, ‘himself‘, ‘after‘, ‘why‘, ‘while‘, ‘can‘, ‘each‘, ‘itself‘, ‘his‘, ‘all‘, ‘once‘,
‘herself‘, ‘more‘, ‘our‘, ‘they‘, ‘hasn‘, ‘on‘, ‘ma‘, ‘them‘, ‘its‘, ‘where‘, ‘did‘, ‘ll‘, ‘you‘,
‘didn‘, ‘nor‘, ‘as‘, ‘now‘, ‘before‘, ‘those‘, ‘yours‘, ‘from‘, ‘who‘, ‘was‘, ‘m‘, ‘been‘, ‘will‘,
‘into‘, ‘same‘, ‘how‘, ‘some‘, ‘of‘, ‘out‘, ‘with‘, ‘s‘, ‘being‘, ‘t‘, ‘mightn‘, ‘she‘, ‘again‘, ‘be‘,
‘by‘, ‘shan‘, ‘have‘, ‘yourselves‘, ‘needn‘, ‘and‘, ‘are‘, ‘o‘, ‘these‘, ‘further‘, ‘most‘, ‘yourself‘,
‘having‘, ‘aren‘, ‘here‘, ‘he‘, ‘were‘, ‘but‘, ‘this‘, ‘myself‘, ‘own‘, ‘we‘, ‘so‘, ‘i‘, ‘does‘, ‘both‘,
‘when‘, ‘between‘, ‘d‘, ‘had‘, ‘the‘, ‘y‘, ‘has‘, ‘down‘, ‘off‘, ‘than‘, ‘haven‘, ‘whom‘, ‘wouldn‘,
‘should‘, ‘ve‘, ‘over‘, ‘themselves‘, ‘few‘, ‘then‘, ‘hadn‘, ‘what‘, ‘until‘, ‘won‘, ‘no‘, ‘about‘,
‘any‘, ‘that‘, ‘for‘, ‘shouldn‘, ‘don‘, ‘do‘, ‘there‘, ‘doing‘, ‘an‘, ‘or‘, ‘ain‘, ‘hers‘, ‘wasn‘,
‘weren‘, ‘above‘, ‘a‘, ‘at‘, ‘your‘, ‘theirs‘, ‘below‘, ‘other‘, ‘not‘, ‘re‘, ‘him‘, ‘during‘, ‘which‘]
人工分词:
这里,英文的分词,直接就是对着空白处分割就可以了。
中文的分词稍微复杂点儿,具体可以百度:CoreNLP, HaNLP, 结巴分词,等等
分词的意义在于,把我们的长长的字符串原文本,转化成有意义的小元素:
texts = [[word for word in doc.lower().split() if word not in stoplist] for doc in doclist]
这时候,我们的texts就是我们需要的样子了:
texts[0]
用词袋的方法,把每个单词用一个数字index指代,并把我们的原文本变成一条长长的数组:
dictionary = corpora.Dictionary(texts) corpus = [dictionary.doc2bow(text) for text in texts]
给你们看一眼:
corpus[13]
这个列表告诉我们,第14(从0开始是第一)个邮件中,一共6个有意义的单词(经过我们的文本预处理,并去除了停止词后)
其中,36号单词出现1次,505号单词出现1次,以此类推。。。
接着,我们终于可以建立模型了:
lda = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=20)
我们可以看到,第10号分类,其中最常出现的单词是:
lda.print_topic(10, topn=5)
‘0.007*kurdistan + 0.006*email + 0.006*see + 0.005*us + 0.005*right‘
我们把所有的主题打印出来看看
lda.print_topics(num_topics=20, num_words=5)
通过
lda.get_document_topics(bow)或者
lda.get_term_topics(word_id)两个方法,我们可以把新鲜的文本/单词,分类成20个主题中的一个。
但是注意,我们这里的文本和单词,都必须得经过同样步骤的文本预处理+词袋化,也就是说,变成数字表示每个单词的形式。
标签:html sel off extract 概率分布 com 步骤 dip 语料库
原文地址:https://www.cnblogs.com/Mjerry/p/9862526.html